1. Surface area of cubes and cuboids

 

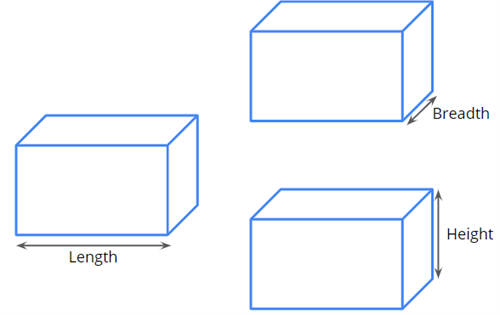
Let us consider a cuboidal cardboard box. Do you know how much cardboard has been used to construct that box?

 

We can find the amount of cardboard used by finding the box's total surface area.

 

First, let us cut open the box.

 

The net of the box looks like this.

 

 

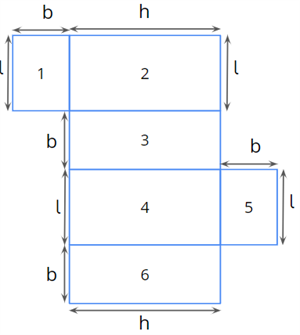
\(\text{The total surface area of the cardboard box}\) \(=\) \(\text{Area}\) \(1\) \(+\) \(\text{Area}\) \(2\) \(+\) \(\text{Area}\) \(3\) \(+\) \(\text{Area}\) \(4\) \(+\) \(\text{Area}\) \(5\) \(+\) \(\text{Area}\) \(6\)

 

\(= (l \times b) + (l \times h) + (b \times h) + (l \times h) + (l \times h) + (l \times b) + (b \times h)\)

 

\(= 2 \times [(l \times b) + (l \times h) + (b \times h)]\)

 

 

What forms the lateral surface of the cuboid?

 

The \(4\) faces (excluding the top and bottom faces) form the lateral surface of the cuboid.

 

Let us look at the representation below.

 

 

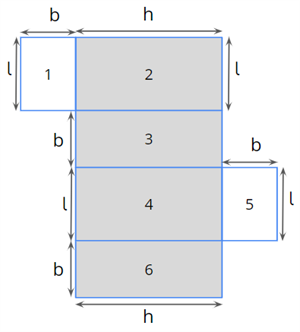
Here, the shaded portion forms the lateral surface of the cuboid.

 

\(\text{The lateral surface of a cuboid}\) \(=\) \(\text{Area}\) \(2\) \(+\) \(\text{Area}\) \(3\) \(+\) \(\text{Area}\) \(4\) \(+\) \(\text{Area}\) \(6\)

 

\(= (l \times h) + (b \times h) + (l \times h) + (b \times h)\)

 

\(= h \times (2l + 2b)\)

 

\(\text{The lateral surface of a cuboid} = 2h \times (l + b)\)

Cube is a special type of cuboid whose length, breadth and height are all equal.

 

 

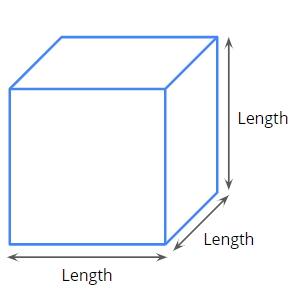
Let us consider the total surface area of the cuboid to find the total surface area of the cube.

 

\(\text{The total surface of a cuboid} = 2 \times [(l \times b) + (l \times h) + (b \times h)]\)

 

Since the length, breadth and height of a cube are equal, we can substitute '\(l\)' in the place of '\(b\)' and '\(h\)'.

 

\(\text{The total surface of a cube} = 2(l \times l + l \times l + l \times l)\)

 

\(= 2(3 \times l^2)\)

 

\(\text{The total surface of a cube} = 6 \times l^2\)

 

Let us now consider the lateral surface area of a cuboid.

 

\(\text{The lateral surface of a cuboid} = 2h \times (l + b)\)

 

Let us now substitute '\(l\)' in the place of '\(b\)' and '\(h\)' to find the lateral surface area of the cube.

 

 

\(= 2l + 2l\)