PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAdjacent vertices: The end-points of the same side of a polygon are called the adjacent vertices.
Adjacent sides: Sides of a polygon that have a common vertex are called adjacent sides. If the sides of a polygon don't have any common vertex is called non-adjacent sides.
Example:
Consider a quadrilateral \(ABCD\).
Here, the vertex \(A\) adjacent to vertex \(B\) in the side \(AB\) and adjacent to vertex \(C\) in the side \(AC\). Thus, the vertex \(A\) is adjacent to the vertex \(B\) as well as the vertex \(C\). But the vertex \(A\) is non-adjacent to the vertex \(D\).
Also, the side \(AB\) is adjacent to side \(BD\) when we consider the common vertex as \(B\), and it is adjacent to the side \(AC\) when we consider the common vertex as \(A\). But the side \(AB\) is non-adjacent to the side \(AD\).
Important!
Diagonals: The line segments obtained by joining vertices which are not adjacent are called the diagonals of a polygon.
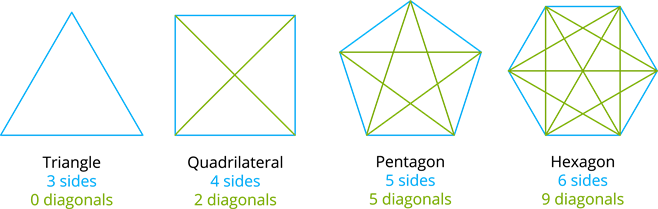
The number of diagonals of a convex polygon: If there are \(n\)-sides in a convex polygon and \(n > 3\), then it has diagonals. A triangle has no diagonals.
Example:
Consider a \(16\)-gon.
Let's find the number of diagonals in it.
We have the number of sides \(n = 16\).
Substitute the value in the formula.
The number of diagonals in \(16\)-gon \(=\) \(= 104\).
Important!
In a triangle, all the sides/vertices are adjacent to each other. Therefore, we cannot draw diagonals in it. Thus, the number of diagonals in any triangle is \(0\).
Register for free to see more content