PDF chapter test TRY NOW
Polygons are classified according to the number of sides (or vertices) as follows:
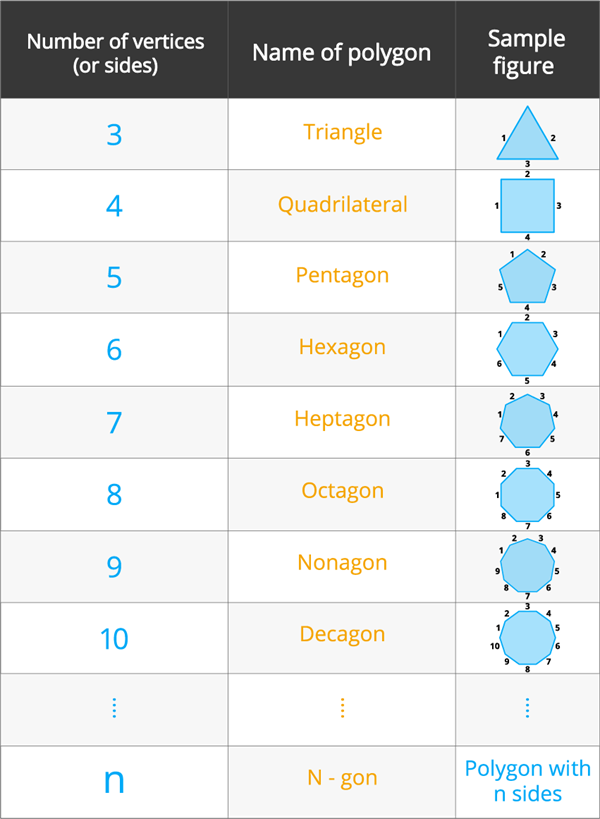
Important!
Here \(n\)-gon denotes the polygon with \('n'\) sides and \('n'\) vertices.
Example:
Concave and convex polygon: If each of the interior angles of a polygon is less than \(180°\), then it is called a convex polygon. If at least one angle of a polygon is more than \(180°\), then it is called a concave polygon.
Example:
Example:
Regular and irregular polygon: A regular polygon is a polygon whose all sides and all angles are equal. Thus, a regular polygon is both equiangular and equilateral.
Example:
Register for free to see more content