PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet's recall some basic definitions about polygons:
Line and Line segments: A line segment is the shortest distance between two points. The line segment joining points \(A\) and \(B\) denoted by . A line can be obtained from a line segment like is extended on both sides indefinitely.
Example:
A curve: Any drawing irrespective of straight or non-straight done without lifting the pen may be called a curve. In general, the 'word' curve means must bend (change direction), but in mathematics, a straight line is also a curve.
Example:
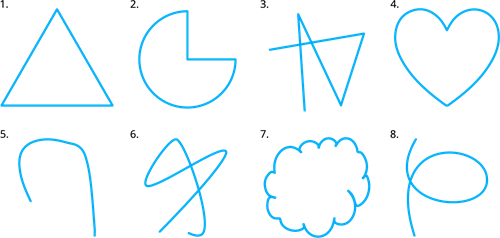
Here all the above figures have been drawn without lifting the pen from the paper. Thus, these are curves.
Simple curve: A simple curve is one that does not cross itself.
Example:
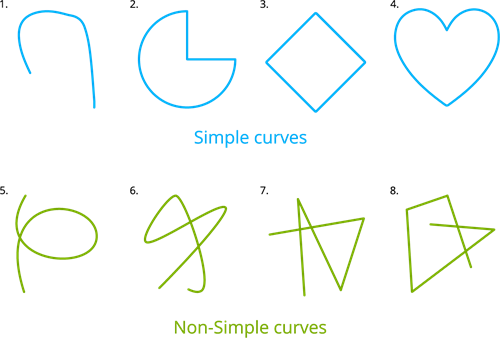
Here the first four figures are examples of simple curves as they didn't overlap itself but the last four figures are examples of non-simple curves as it overlaps itself.
Open and closed curve: A curve is said to be closed if it ends are joined; otherwise, it is said to be open.
Example:
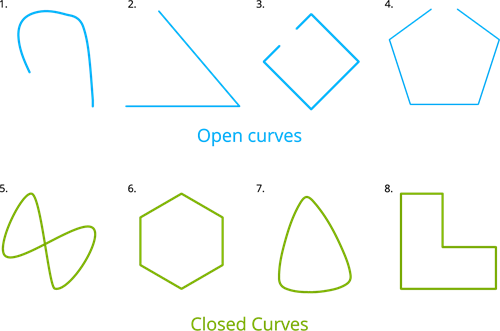
Here the first four figures are examples of open curves as they are not closed but the last four figures are examples of closed curves.
Important!
In a closed curve, there are three parts. They are:
1. interior (‘inside’) of the curve
2. boundary (‘on’) of the curve and
3. exterior (‘outside’) of the curve
2. boundary (‘on’) of the curve and
3. exterior (‘outside’) of the curve
The interior of a curve together with its boundary is called its “region”.
Example:
Consider the following figure.
In here, interior and exterior region are mentioned in blue shade and the boundary line has been drawn in black lines.
Important!
Simple closed curves are the curve which closed (end points are closed) as well as one that does not cross itself (simple).
Polygon: It is a simple closed curve made up of line segments.
Example:
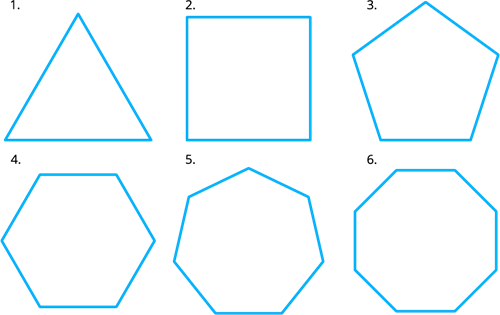
In here, the above all six figures are polygons. Polygon is made up of line segments. Triangle is the smallest polygon made up of three line segments, a quadrilateral is a polygon made up of four line segments, a pentagon is made up of five line segments and so on.
Register for free to see more content