UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreThere are some properties which are always true for any parallelogram.
Let's see those properties with explanation.
In a parallelogram, the following properties are true:
- the opposite sides are equal in length.
- the opposite angles are equal in measure.
- the adjacent angles are supplementary.
- the diagonals bisect each other.
Proof:
Let's prove (1) and (2).
Let \(ABCD\) be a parallelogram.
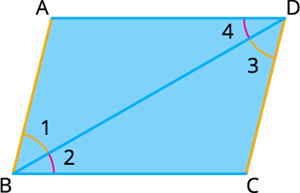
Draw a diagonal \(BD\) and denote the interior angles as \(∠1, ∠2, ∠3\) and \(∠4\).
Since \(ABCD\) is a parallelogram, \(AD\) is parallel to \(BC\) and \(AB\) is parallel to \(CD\).
Consider the parallel lines \(AD\) and \(BC\) and take the diagonal \(BD\) as transversal.
Here \(∠2 = ∠4\) by alternate interior angle property [Alternate interior angles are equal in measure].
Now consider parallel lines \(AB\) and \(CD\) and take the diagonal \(BD\) as transversal.
Here \(∠1 = ∠3\) by alternate interior angle property [Alternate interior angles are equal in measure].
So we have \(∠1 + ∠2 = ∠3+∠4\). That is, \(∠B = ∠D\).
Consider the triangles \(DAB\) and \(BCD\) with the common side \((BD = BD)\).
Now we have \(∠2 = ∠4\), \(∠1 = ∠3\) and the common side \((BD = BD)\).
By \(ASA\) criterion of congruence, \(DAB\) \(BCD\).
That is, they are congruent triangles.
Therefore, \(AD = BC, AC = CD\) and \(∠A= ∠C\).
Hence, in parallelogram \(ABCD\), we have \(AD = BC, AC = CD, ∠A = ∠C\) and \(∠B = ∠D\).
This proves (1) and (2).
From (2), it is obvious that \(∠A = ∠C\) and \(∠B = ∠D\).
Let's prove (3).
Let the measure of angles are\(∠A = ∠C = x\) and \(∠B = ∠D = y\).
We have the property that sum of all interior angles of a quadrilateral is \(360°\).
That is, \(∠A + ∠B +∠C + ∠D = 360°\).
Substituting the taken values in the above equation.
\(x + y + x + y = 360°\)
\(2x +2y = 360°\)
\(2(x + y) = 360°\)
\(x + y = 180°\).
That is, we can write this as \(∠A + ∠B = 180°\), \(∠B + ∠C = 180°\), \(∠C + ∠D = 180°\) and \(∠A + ∠D = 180°\).
It proves the property (3).
Let's prove (4).
Consider a parallelogram \(ABCD\). Draw its diagonals \(AC\) and \(BD\). Let the intersection point of the diagonals be \(O\).
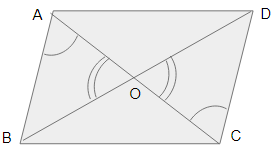
In triangle \(AOB\) and \(COD\), we have:
\(AB = CD\) as opposite sides are equal in parallelogram.
\(∠AOB = ∠COD\) [Because vertically opposite angles are equal].
Here \(AB\) is parallel to \(CD\), so \(∠OAB = ∠DCO\).
By AAS criterion of congruence, \(OAB\)\(OCD\).
This implies, \(OA = OC\) and \(OB = OD\).
As they are equal, diagonals of a parallelogram bisect each other.