Parallelogram and its elements. — lesson. Mathematics CBSE, Class 8.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

A parallelogram is a quadrilateral whose opposite sides are parallel and equal.

Here \(ABCD\) is a parallelogram.

The side \(AB\) is parallel to the side \(CD\) and the side \(AD\) is parallel to the side \(BC\).

Also, the length \(AB = CD\) and \(AD = BC\).

Example:

Consider the parallelogram \(PQRS\) with its sides measures \(6 cm\) and \(8 cm\).

In here the side \(PQ\) is parallel to \(RS\) and the side \(PS\) is parallel to \(QR\).

Also, it is clear that the length \(PQ = RS = 6 cm\) and the length \(PS = QR = 8 cm\).

Elements of parallelogram:

Parallelogram is made up of four sides and four angles. There are some terms we usually use to denote parallelogram.

They are:

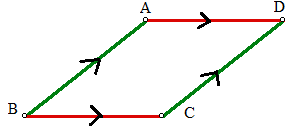
Let's see the elements of the parallelogram \(ABCD\).

The side \(AB\) is opposite to the side \(CD\) and the side \(AD\) is opposite to the side \(BC\).
The angle \(A\) is opposite to the angle \(C\) and the angle \(B\) is opposite to the angle \(D\).
The side \(AB\) is adjacent to the side \(BC\) because one of the sides starts where the other ends. In here, the side \(AB\) ends at the vertex \(B\) and the side \(BC\) starts from there.
The angles \(A\) and \(B\) are adjacent angles as they are at the ends of the same side \(AB\).

Did you find an error?

1. Parallelogram and its elements.