PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA parallelogram with all sides are equal is called a rhombus.
Now we are going to define a rhombus \(ABCD\) as a quadrilateral is a parallelogram with all the sides are in equal measures.
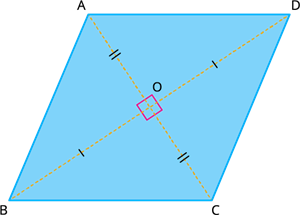
Thus, if \(ABCD\) is a rhombus then \(AB = BC = CD = AD\), \(AB || CD\) and \(BC || AD\).
Important!
Rhombus is a special case of kite. Note that the sides of a rhombus are all of the same length; this is not the case with the kite.
A rhombus has all the properties of a parallelogram and also that of a kite.
In a rhombus, the following properties are true:
- The sum of all the four angles of the rhombus is equal to \(360°\).
- The opposite sides are equal in length.
- The opposite angles are equal in measure.
- The adjacent angles are supplementary.
- The diagonals are perpendicular bisector of each other.
Register for free to see more content