PDF chapter test TRY NOW

4. Concept of rectangle

A parallelogram whose each angle is a right angle is called a rectangle.
Now we are going to define a rectangle \(ABCD\) as a quadrilateral is a parallelogram whose each interior angle is \(90°\).
 
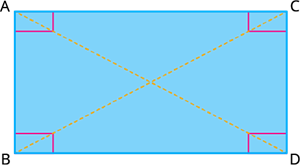
Theory_4_1.png
 
Thus, if \(ABCD\) is a rectangle then \(AB=BC=CD=AD\) and \(AB||CD\) and \(BC||AD\).
Important!
A rectangle has all the properties of a parallelogram with interior.
In a rectangle, the following properties are true:
  1. The opposite sides are parallel and equal in length.
  2. The interior angles of the rectangle is \(90°\).
  3. The diagonals are equal in measure and bisect each other.
  4. The adjacent angles are supplementary.
Previous theory
Exit to the topic
Next theory
Register for free to see more content
Register now
Copyright © 2024 YaClass Tech Private Limited Contacts Terms and Conditions Privacy Policy