PDF chapter test TRY NOW
Before getting into a deeper study of lines and angles, let us first recall a few basic terms and definitions.
1. A line does not have endpoints. A line \(AB\) is denoted by \(\overleftrightarrow{AB}\).
2. A line with two endpoints is a line segment. A line segment \(AB\) is denoted by \(\overline {AB}\).
3. A line with only one endpoint is a ray. A ray is denoted by \(\overrightarrow{AB}\).
4. If three or more points lie on the same line, it is called collinear points.
5. The points that don't lie on the same line are called non-collinear points.
6. Two rays originate from the same point to form an angle. The two rays forming an angle are called arms, and the point from which they originate is the vertex of the angle.
7. Angles measuring between \(0^\circ\) and \(90^\circ\) are acute angles. Similarly, angles measuring between \(90^\circ\) and \(180^\circ\) are obtuse angles. An exact \(90^\circ\) angle is a right angle. An exact \(180^\circ\) angle is a straight angle. Also, the angles that exceed \(180^\circ\) are called reflex angles.
8. When the sum of two angles measures lesser than \(90^\circ\), they are called complementary angles. Similarly, when the sum of two angles measures lesser than \(180^\circ\), they are called supplementary angles.
9. When a ray is common among two angles, and the non-common arms of the two angles form a straight line, then they are called linear pair of angles.
10. When two lines meet each other, they are called intersecting lines. When two lines do not meet each other, they are called non-intersecting lines or parallel lines.
11. When two lines intersect at \(O\), then \(O\) generates two vertically opposite angles.
12. The lines that intersect two or more lines at unique points are called transversal lines.
Axioms supporting linear pair of angles
Axiom \(1\): If a ray stands on a line, then the sum of two adjacent angles so formed is \(180^\circ\).
Given: A ray stands on a line.
Conclusion: The sum of two adjacent so formed is \(180^\circ\).
Now, let us try to swap both 'Given' and 'Conclusion'. Now, 'Given' becomes 'The sum of two adjacent so formed is \(180^\circ\)', and 'Conclusion' becomes 'A ray stands on a line'.
Now the newly formed statement becomes, 'When the sum of two adjacent so formed is \(180^\circ\), a ray stands on the line.' We have just reversed the original axiom. Hence, this statement is also known as the converse of axiom \(1\).
We don't know whether the converse of the axiom is true or not.
Let us try to verify the converse of axiom \(1\).

A \(180^\circ\) angle is a straight angle. Using the four figures given above, let us check if any of the non-common arms together form a straight line or not.

The non-common arms of figure \(3\) form a straight line.
Hence, the converse of axiom \(1\) is verified.
Axiom \(2\): If the sum of two adjacent angles is \(180°\), then the non-common arms of the angles form a line.
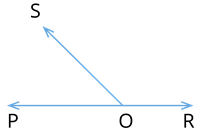
From the figure given above, let \(\angle POS = x^\circ\), and \(\angle SOR = (180 - x)^\circ\).
\(\angle POR = \angle POS + \angle SOR = x + 180 - x = 180^\circ\)
The angles \(\angle POS\) and \(\angle SOR\) together form \(180^\circ\).
The ray \(OS\) is common among both the angles \(\angle POS\), and \(\angle SOR\).
Hence, \(OS\) is the ray on the line \(POR\).
\(POR = PO + OR\) \(\longrightarrow (1)\)
From the figure, we know that \(PO\) and \(OR\) are the non-common arms.
Since \(POR\) forms a straight line, it is understood from \((1)\) that the non-common arms \(PO\) and \(OR\) together form a straight line.
Thus, axiom \(2\) is verified.
