PDF chapter test TRY NOW
Let us discuss how to determine the nature of the solutions for the given quadratic equations.
Example:
1. Find the nature of the solution of the equation \(y = x^2 - 2x - 3\).
Solution:
Step 1: Draw the graph of the equation \(y = x^2 - 2x - 3\).
The table of values for the equation \(y = x^2 - 2x - 3\) is:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(x^2\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) | \(9\) | \(16\) |
| \(2x\) | \(-4\) | \(-2\) | \(0\) | \(2\) | \(4\) | \(6\) | \(8\) |
| \(3\) | \(3\) | \(3\) | \(3\) | \(3\) | \(3\) | \(3\) | \(3\) |
| \(y\) | \(5\) | \(0\) | \(-3\) | \(-4\) | \(-3\) | \(0\) | \(5\) |
Step 2: Plot the points in the graph using a suitable scale.
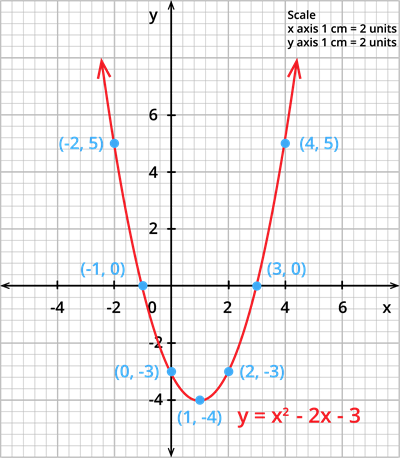
Step 3: Join the points by a smooth curve.
Step 4: In the graph, observe that the curve intersects the \(X\) - axis at \(2\) points \((-1,0)\) and \((3,0)\). Therefore, the roots of the equation are \(-1\) and \(3\).
Since there are two points of intersection with the \(X\) - axis, the given equation has real and unequal roots.
2. Find the nature of the solutions of the equation \(y = x^2 - 10x + 25\).
Solution:
Step 1: Draw the graph of the equation \(y = x^2 - 10x + 25\).
The table of values for the equation \(y = x^2 - 10x + 25\) is given by:
| \(x\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
| \(x^2\) | \(9\) | \(16\) | \(25\) | \(36\) | \(49\) |
| \(10x\) | \(30\) | \(40\) | \(50\) | \(60\) | \(70\) |
| \(25\) | \(25\) | \(25\) | \(25\) | \(25\) | \(25\) |
| \(y\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Step 2: Plot the points in the graph.
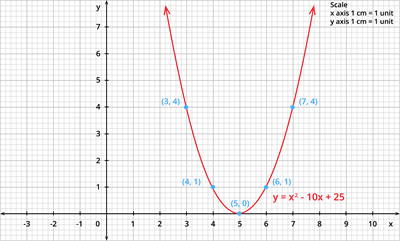
Step 3: Join the points by a smooth curve.
Step 4: Here, the curve meets the \(X\) - axis at only one point. Therefore, the point of intersection of the parabola with \(X\) - axis for the given equation is \((5,0)\).
Since the point of intersection is only one point with \(X\) - axis, the given quadratic equation has real and equal roots.
Register for free to see more content