PDF chapter test TRY NOW
The long division method is used only when the polynomial cannot be factored easily. In general, the long division method is used when the degrees of the polynomial are higher.
Before proceeding with the long division method, arrange the given polynomial in ascending or descending order of the degrees of the variables.
Let us understand how to find the square root of a polynomial by the long division method.
Example:
Find the square root of \(9x^4 + 12x^3 + 10x^2 + 4x + 1\).
Solution:
Step 1: Group the terms as a pair from the unit place. That is, \(9x^4 + \overline{12x^3 + 10x^2} + \overline{4x + 1}\).
Step 2: Here, the extreme left number is \(9x^4\). We must select the number whose square is equal to or less than the given number. Here, the square of the square of the number is \(3x^2\).
Thus, we have:
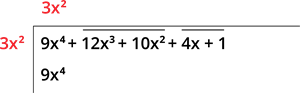
Step 3: Subtracting the numbers, we get \(0\), and bring the next pair to the right of the remainder.
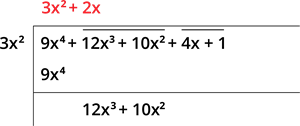
Step 4: Find the new divisor by multiplying the quotient by \(2\). And, the next digit can be selected which is less than or equal to the given term \(12x^3 + 10x^2\).
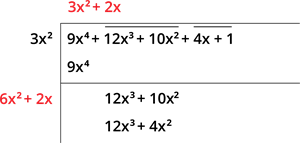
Step 5: Subtract the numbers and write the result, and bring the next pair to the right of the remainder.
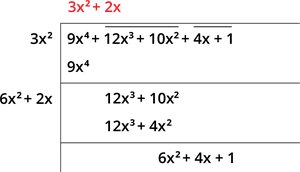
Step 6: Find the new divisor by multiplying the quotient by \(2\). And, the next digit can be selected which is equal to the given term \(6x^2 + 4x + 1\).
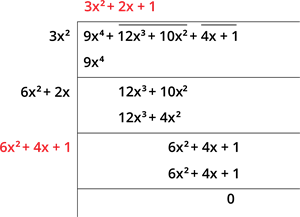
Therefore, \(\sqrt{9x^4 + 12x^3 + 10x^2 + 4x + 1} = |3x^2 + 2x + 1|\).
Register for free to see more content