UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreA cylinder emptied from the inner side and has a difference in the outer and inner radius of a cylinder with the same height is called a hollow cylinder.
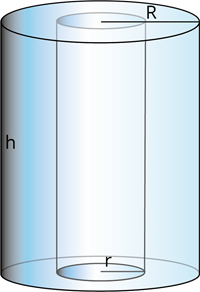
Properties of hollow cylinder:
1. The inner and outer radius of the hollow cylinder is different.
2. The inner and outer lateral surface areas of the hollow cylinders are different.
3. The height of the inner and outer cylinders are the same.
Curved surface area of a hollow cylinder:
Let \(R\) be the outer radius, \(r\) be the inner radius, and \(h\) be the height of the hollow cylinder.
C. S. A. \(=\) Curved surface area of outer cylinder \(+\) Curved surface area of the inner cylinder
\(=\) \(2 \pi R h\) \(+\) \(2 \pi r h\)
\(=\) \(2 \pi (R + r)h\)
Curved surface area of a hollow cylinder \(=\) \(2 \pi (R + r)h\) sq. units
Total surface area of a hollow cylinder:
T. S. A. \(=\) Curved surface area \(+\) Area of a top circular ring \(+\) Area of a bottom circular ring
\(=\) \(2 \pi (R + r)h\) \(+\) \(\pi (R^2 - r^2)\) \(+\) \(\pi (R^2 - r^2)\)
\(=\) \(2 \pi (R + r)h\) \(+\) \(2\pi (R^2 - r^2)\)
\(=\) \(2 \pi (R + r)h\) \(+\) \(2\pi (R + r) (R - r)\)
\(=\) \(2 \pi (R + r) [h + (R - r)]\)
\(=\) \(2 \pi (R + r) (R - r + h)\)
Total surface area of a hollow cylinder \(=\) \(2 \pi (R + r) (R - r + h)\) sq. units
Register for free to see more content