UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreHollow cylinder:
A cylinder emptied from the inner side and has a difference in the outer and inner radius of a cylinder with the same height is called a hollow cylinder.
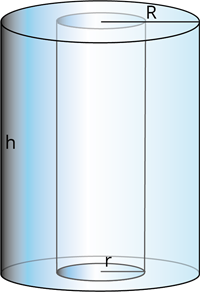
Volume of a hollow cylinder:
Let \(R\) be the outer radius, \(r\) be the inner radius, and \(h\) be the height of the hollow cylinder.
Volume \(=\) Volume of the outer cylinder \(-\) Volume of the inner cylinder
\(=\) \(\pi R^2 h - \pi r^2 h\)
\(=\) \(\pi (R^2 - r^2) h\)
Volume of a hollow cylinder \(=\) \(\pi (R^2 - r^2) h\) cu. units.
Example:
Find the volume of the hollow cylinder of height \(14\) \(cm\) and whose internal and external radii are \(6\) \(cm\) and \(8\) \(cm\), respectively.
Solution:
Internal radius, \(r\) \(=\) \(6\) \(cm\)
External radius, \(R\) \(=\) \(8\) \(cm\)
Height, \(h\) \(=\) \(14\) \(cm\)
Volume of a hollow cylinder \(=\) \(\pi (R^2 - r^2) h\) cu. units.
\(=\)
\(=\)
\(=\)
\(=\) \(22 \times 4 \times 14\)
\(=\) \(1232\)
Therefore, the volume of a hollow cylinder is \(1232\) \(cm^3\).
Important!
The value of \(\pi\) should be taken as unless its value is shared in the problem.
Register for free to see more content