Congruence modulo — lesson. Mathematics State Board, Class 10.

PDF chapter test TRY NOW

Two integers,

$a$ and

$b$ , are said to be congruent modulo

$n$ if and only if their difference is divisible by

$n$ . It can be written as

$a \equiv b (mod \ n)$

In other words, the two integers,

$a$ and

$b$ , is the difference of the integer multiple of congruence modulo

$n$ . That is,

$b - a = kn$ for some integer

$k$ .

Here,

$n$ is called the modulus of the congruence.

Example:

$39 \equiv 4 (mod \ 5)$ . Here,

$5$ is the modulus of the congruence because

$39 - 4 = 35$ is divisible by

$5$ .

Consider the following examples on how to find the congruence modulo.

Example:

1. Find

$3 (mod \ 2)$

Solution:

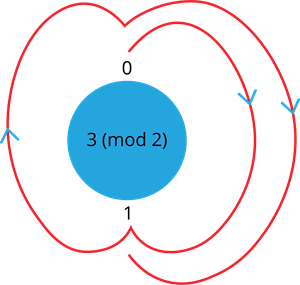
Consider the possible remainders for the number with mod

$2$ are

$0$ ,

$1$ .

To find the remainder of the given number, start at

$0$ and go through

$3$ numbers in a clockwise direction. The

$3$ numbers would go in a cycle starting from

$0$ . They are

$1$ ,

$0$ ,

$1$ . Since the cycle ends at the remainder of

$1$ , the answer for

$3 (mod \ 2)$ is

$1$ .

Therefore,

$3 \equiv 1 (mod \ 2)$

2. Find

$-3 (mod \ 2)$

Solution:

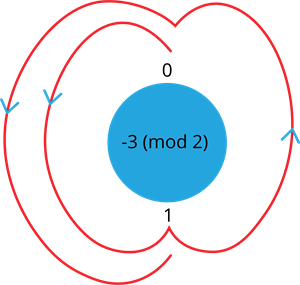
Consider the possible remainders for the number with mod

$2$ are

$0$ ,

$1$ .

To find the remainder of the given number, start at

$0$ and go through

$3$ numbers in a anticlockwise direction(because the number has a negative sign). The

$3$ numbers would go in a cycle starting from

$0$ . They are

$1$ ,

$0$ ,

$1$ . Since the cycle ends at the remainder of

$1$ , the answer for

$-3 (mod \ 2)$ is

$1$ .

Therefore,

$-3 \equiv 1 (mod \ 2)$

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

2. Congruence modulo

Theory: