PDF chapter test TRY NOW
A function is a relationship that exists between two non-empty sets.
Let us consider the following situation:
In a locality, we can classify \(5\) houses based on their rents. The relationship between the houses and their rents is depicted in the figure that follows.

From the figure, we can understand that all \(5\) houses have five different rents. In other words, each of the houses has a unique rent.
Example:
Let us look at a few more examples involving functions.
1. Day-to-day weather forecast: A day can have only one average temperature.
2. The total number of steps walked in a day: There can only be one number corresponding to each day.
3. The number of goals saved in a football match: The number obtained cannot vary.

In the examples given above, each input will have only one output. These relations are called functions.
Function:
A relation \(f\) between two non-empty sets \(X\) and \(Y\) is called a function from \(X\) to \(Y\) if, for each \(x \in X\), there exists only one \(y \in Y\) such that \((x, y) \in f\).
That is, \(f\) \(=\) \(\{(x, y)\)\(|\) for all \(x \in X\),\(y \in Y\).
A function is made of relations, but all relations are not functions.
1. Functions are subsets of relations.
2. Relations are subsets of cartesian products.
Let us look at the representation given below for a better understanding.

A function \(f\) can be thought of as a mechanism (or device) which gives a unique output \(f(x)\) to every input \(x\).
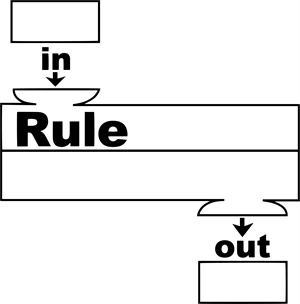
Example:
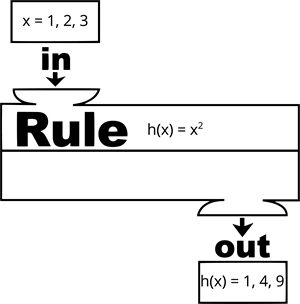
Consider the set \(A = \{1,2,3\}\) and the set \(B = \{1,4,9\}\) and the funcction \(h\) is defined as the '\(h(x) = x^2\)' from the set \(A\) to the set \(B\).
Let us check whether this function satisfies the definition or not.
Here, the sets \(A\) and \(B\) are non-empty sets.
\(h\) is a function from \(A\) to \(B\).
\(h(1)\) \(= (1)^2 = 1\)
\(h(2)\) \(= (2)^2 = 4\)
\(h(3)\) \(= (3)^2 = 9\)
According to the definition, there exist a unique element(\(1, 4, 9\)) in set \(B\) for each element(\(1,2,3\)) of set \(A\) such that \((1,1), (2,4), (3,9)\) in the function \(h\).
Important!
- The function \(f\) from \(X\) to \(Y\) can also be written as \(f : X \rightarrow Y\).
- A function is also known as mapping or transformation.
- All functions are relations, but all relations are need not be a function.
