
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoConsider, you went to a shop with your friend. You bought \(7\) chocolates for both of you. You and your friends ate three chocolates and decided to split the last one chocolate equally.
So each one ate \(3\) chocolates and \(\frac{1}{2}\) chocolate this can be written as
In terms of improper fraction, we can say that you both had chocolates, and in terms of mixed fraction we can say that, you both had eaten chocolates.
Mixed fractions contain a whole number and a proper fraction. They can also be represented as an improper fraction.
Example:
; where \(4\) is a whole number and \(\frac{10}{5}\) is a proper fraction.
Let us see how to convert the mixed fraction to improper fraction and vice versa.
Converting mixed fraction to improper fraction:
Apply the following steps to convert a mixed fraction to improper fraction.
Step 1: Multiply the denominator of the proper fraction and whole number and add it with the numerator of the fraction to get the numerator of the improper fraction.
Step 2: Denominator of an improper fraction is the same as the denominator of a mixed fraction.
Example:
Convert to an improper fraction.
Step 1: Numerator of improper fraction \(=\) (denominator of the proper fraction \(×\) whole number) \(+\) numerator of a proper fraction.
\(= 5 × 4 = 20 + 10 = 30\)
Step 2: Denominator of improper fraction \(=\) denominator of the mixed fraction.
The denominator of improper fraction \(= 5\).
Improper fraction \(= \frac{30}{5}\).
Thus, \(= \frac{30}{5}\) \(= 6\).
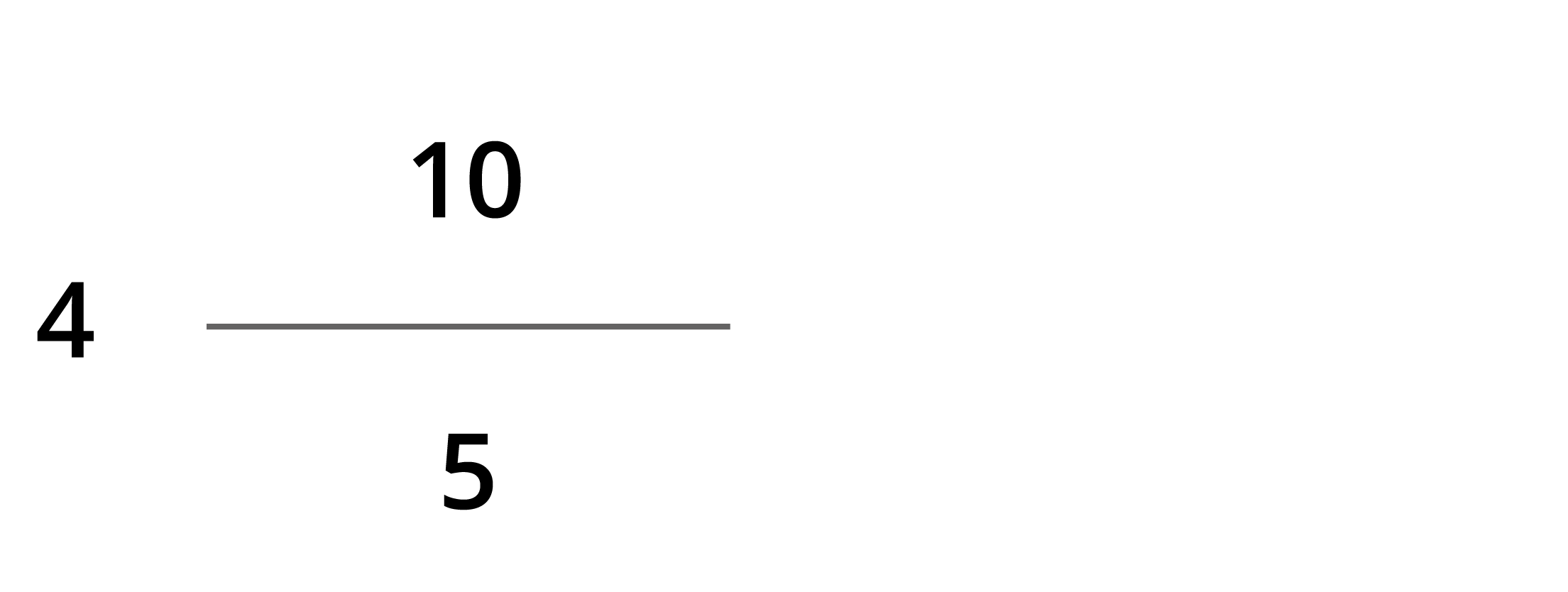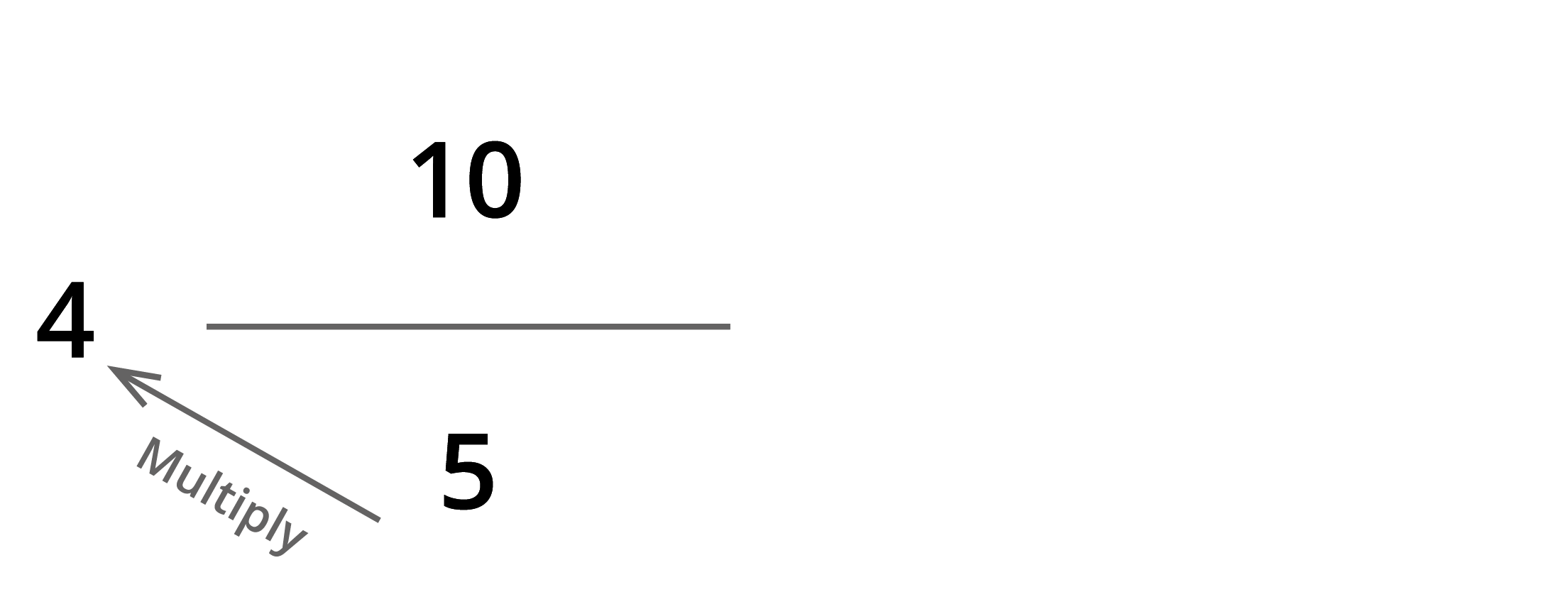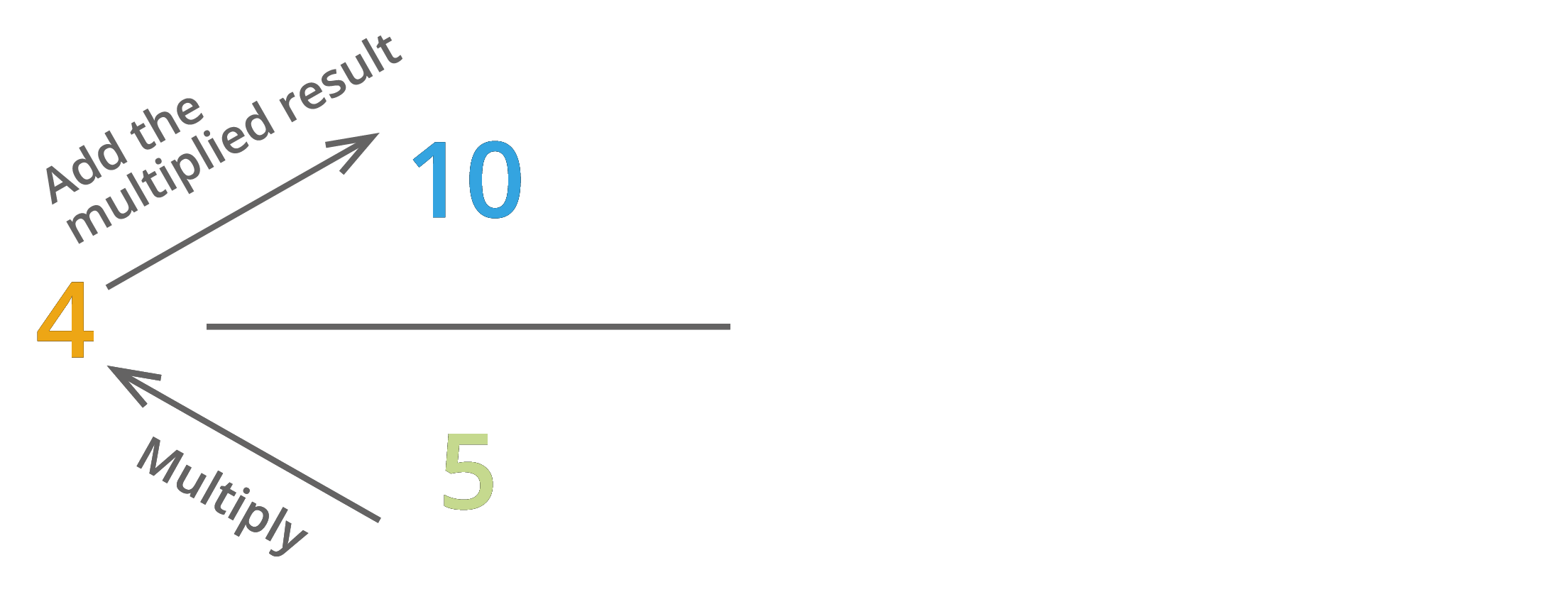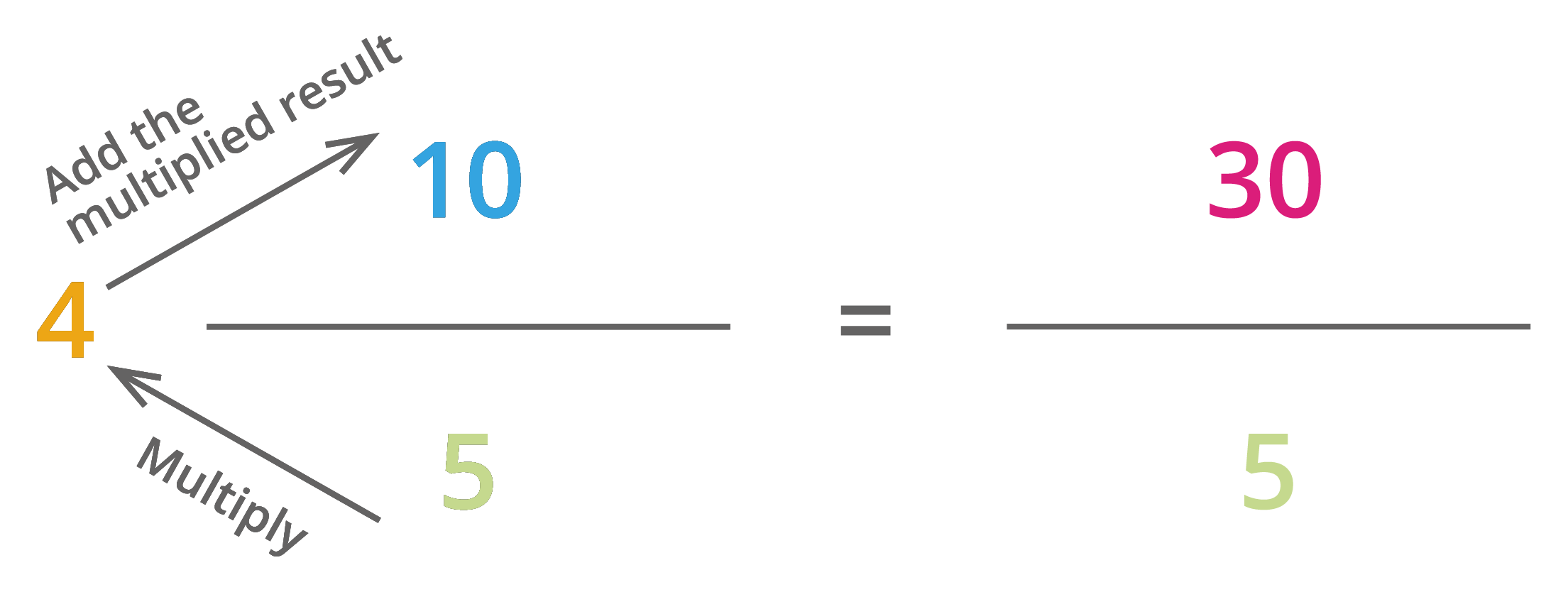
Converting improper fraction to mixed fraction:
We can express an improper fraction as a mixed fraction by dividing the numerator by denominator to obtain the quotient and remainder.
Divide the given fraction and find the quotient and remainder.
The quotient of the division \(=\) The whole number in mixed fraction.
The remainder of a division \(=\) The numerator of mixed fraction.
The denominator of the improper fraction \(=\) The denominator of mixed fraction.
\(\text{Quotient}\) \(+\) \(\frac{\text{Remainder}}{\text{Divisor}}\) \(=\) \(\text{Quotient}\) \(\frac{\text{Remainder}}{\text{Divisor}}\)
Example:
Let us convert the fraction \(\frac{11}{5}\) to a mixed fraction.

The remainder is \(1\), the quotient is \(2\).
The whole number in mixed fraction \(=\) quotient of division \(= 2\)
The numerator of mixed fraction \(=\) reminder of division \(= 1\)
The denominator of mixed fraction \(=\) denominator of improper fraction \(= 5\)
Thus, \(\frac{11}{5} =\) .