PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoDraw a line perpendicular to the given line at a point on a line.
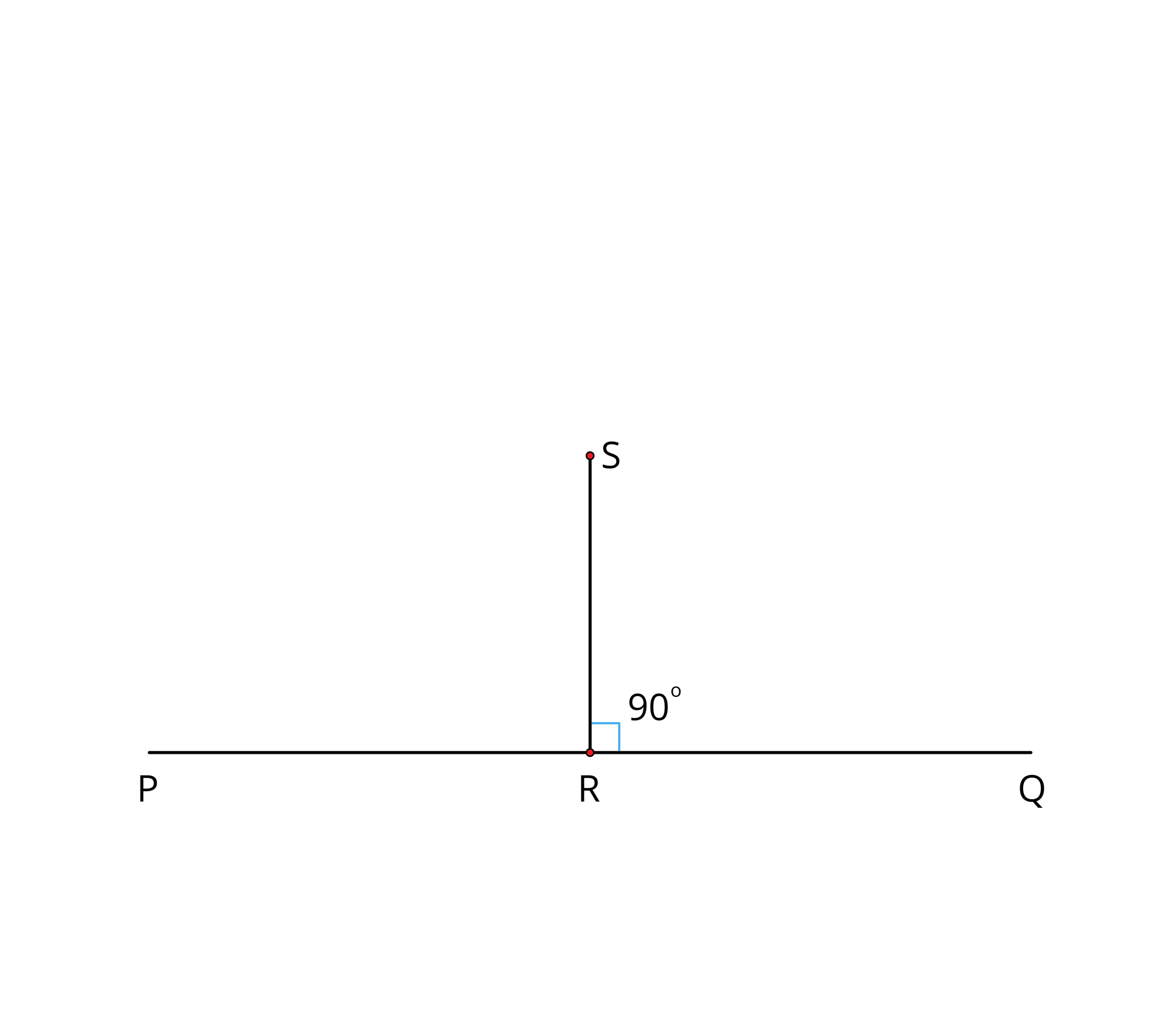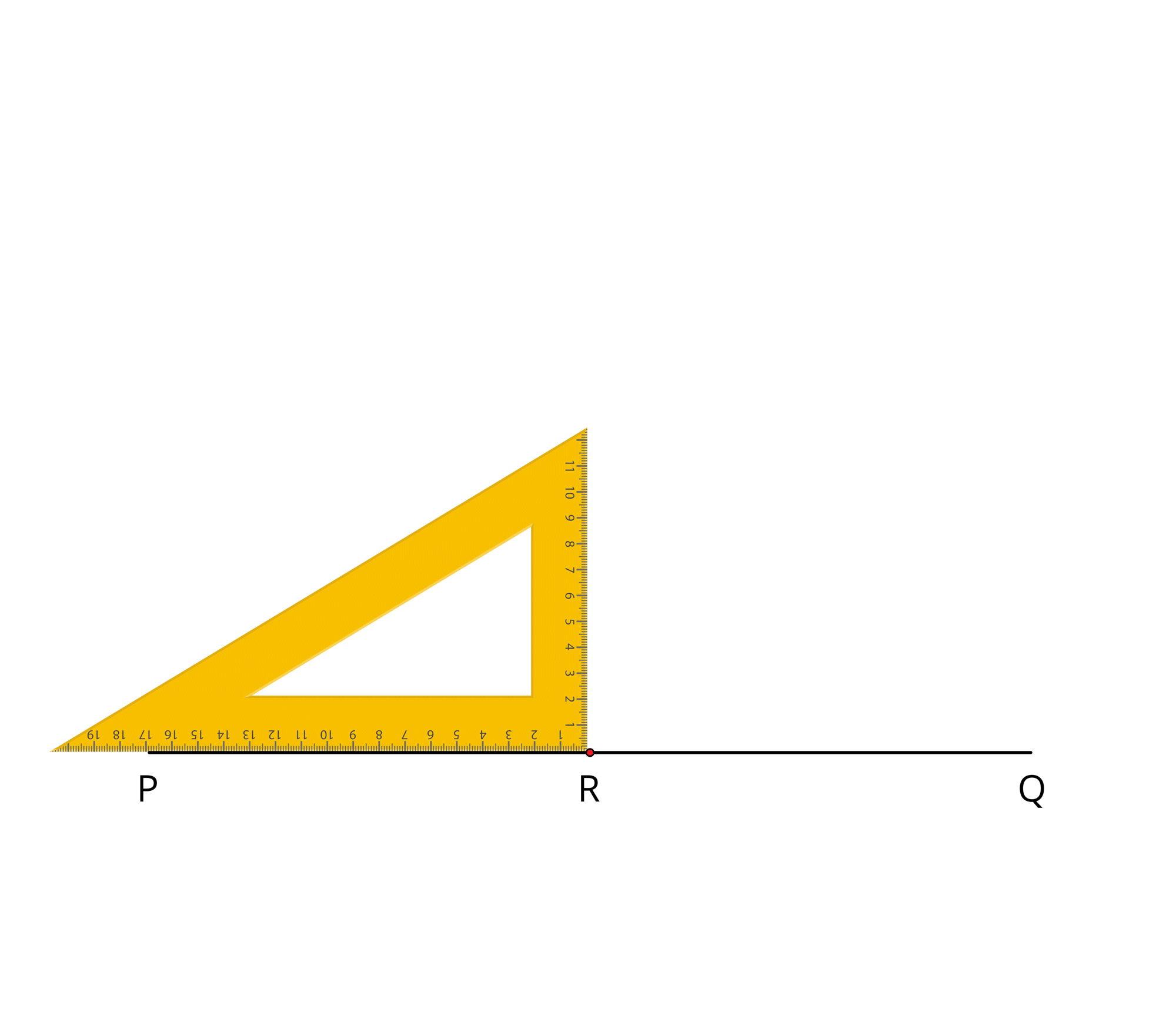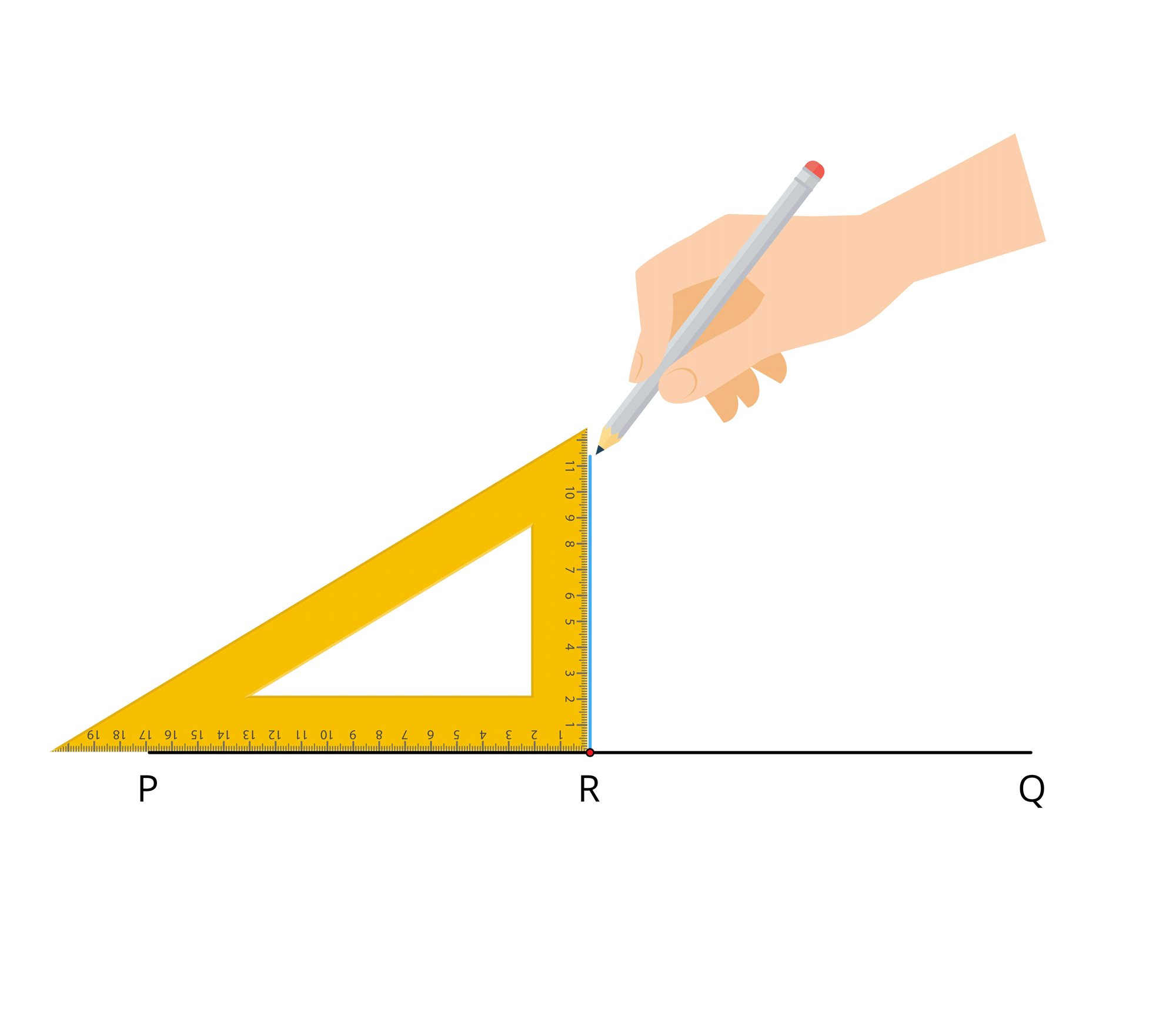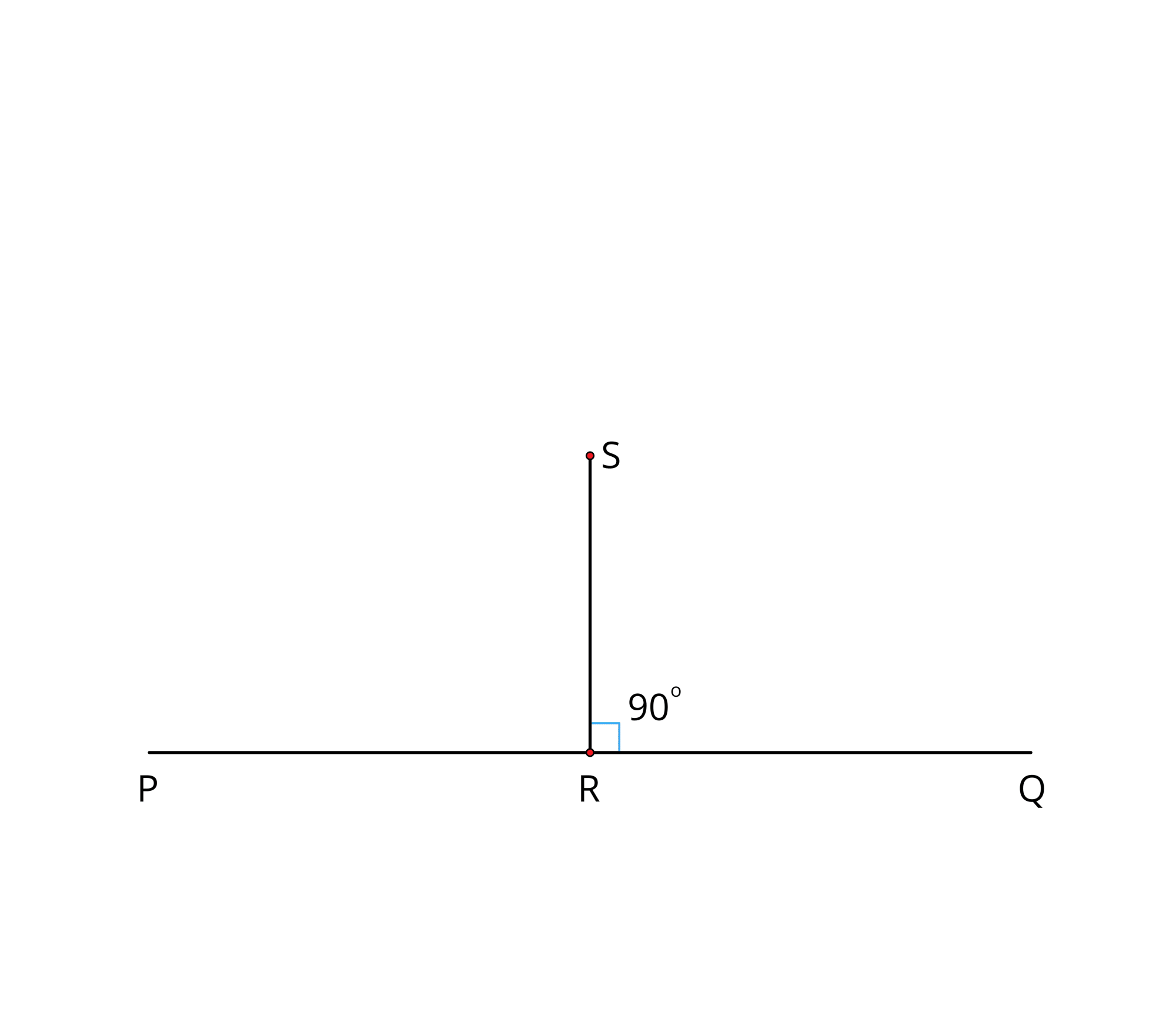
Step \(1\): Draw a line \(PQ\).
Step \(2\): Take a point \(R\) anywhere on the line \(PQ\).
Step \(3\): Place the set square on the line in such a way that the vertex which forms right angle coincides with \(R\) and one arm of the right angle coincides with the line \(PR\).
Step \(4\): Draw a line \(RS\) through \(R\) along the other arm of the right angle of the set square.
Step \(5\): The line \(RS\) is perpendicular to the line \(PQ\) at \(R\). That is, \(RS \perp PQ\) and \(\angle SRP = \angle SRQ = 90°\).
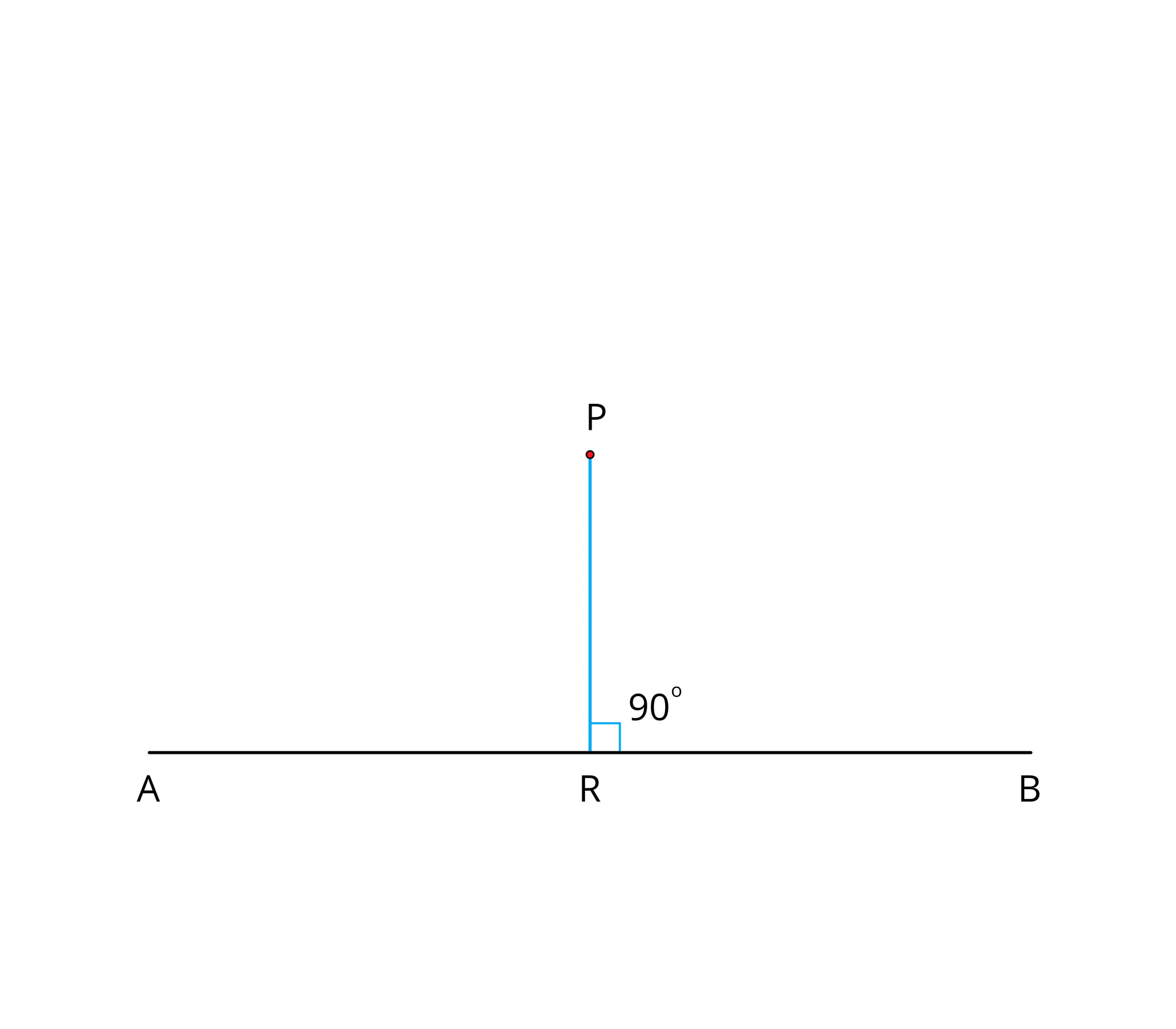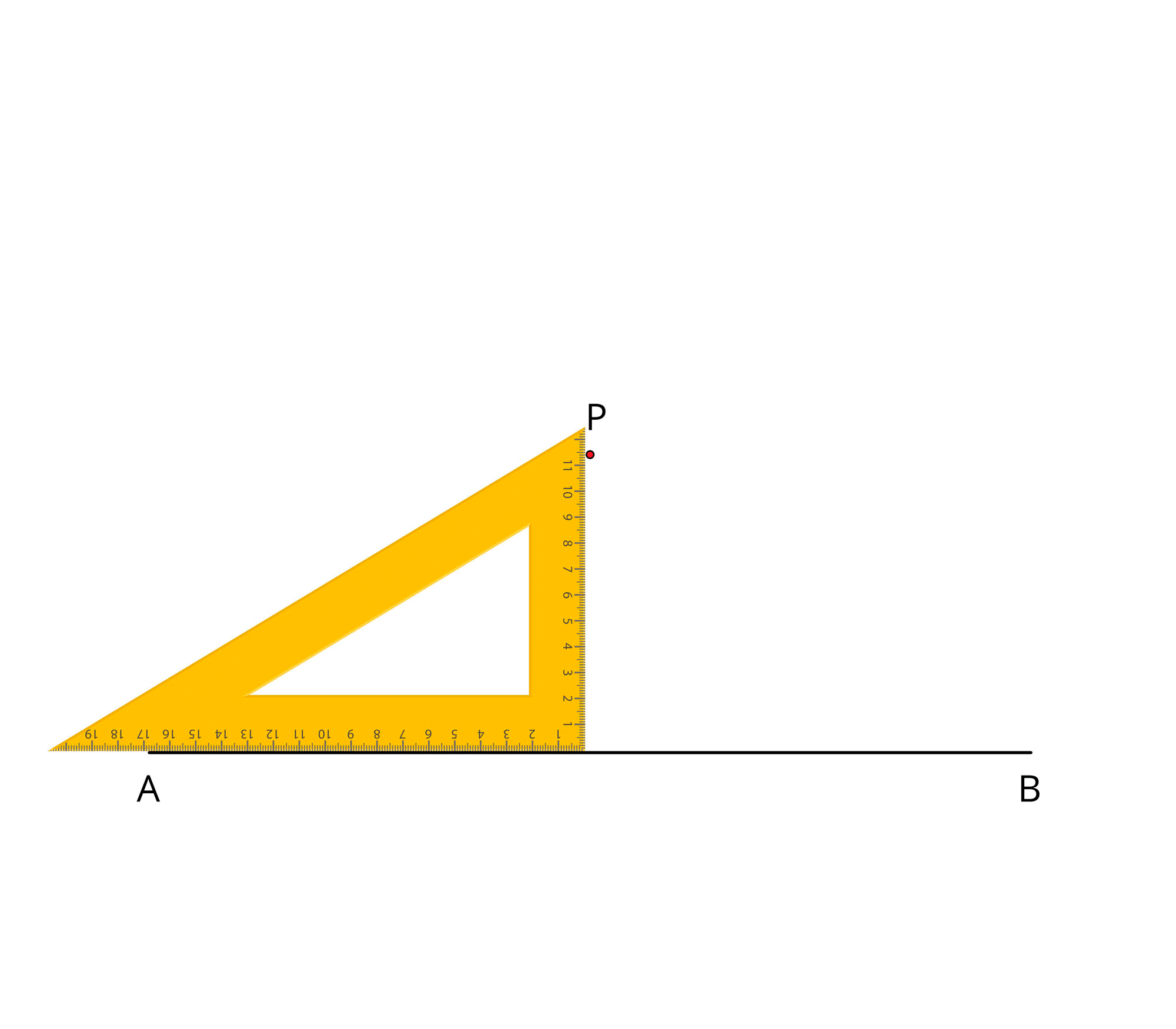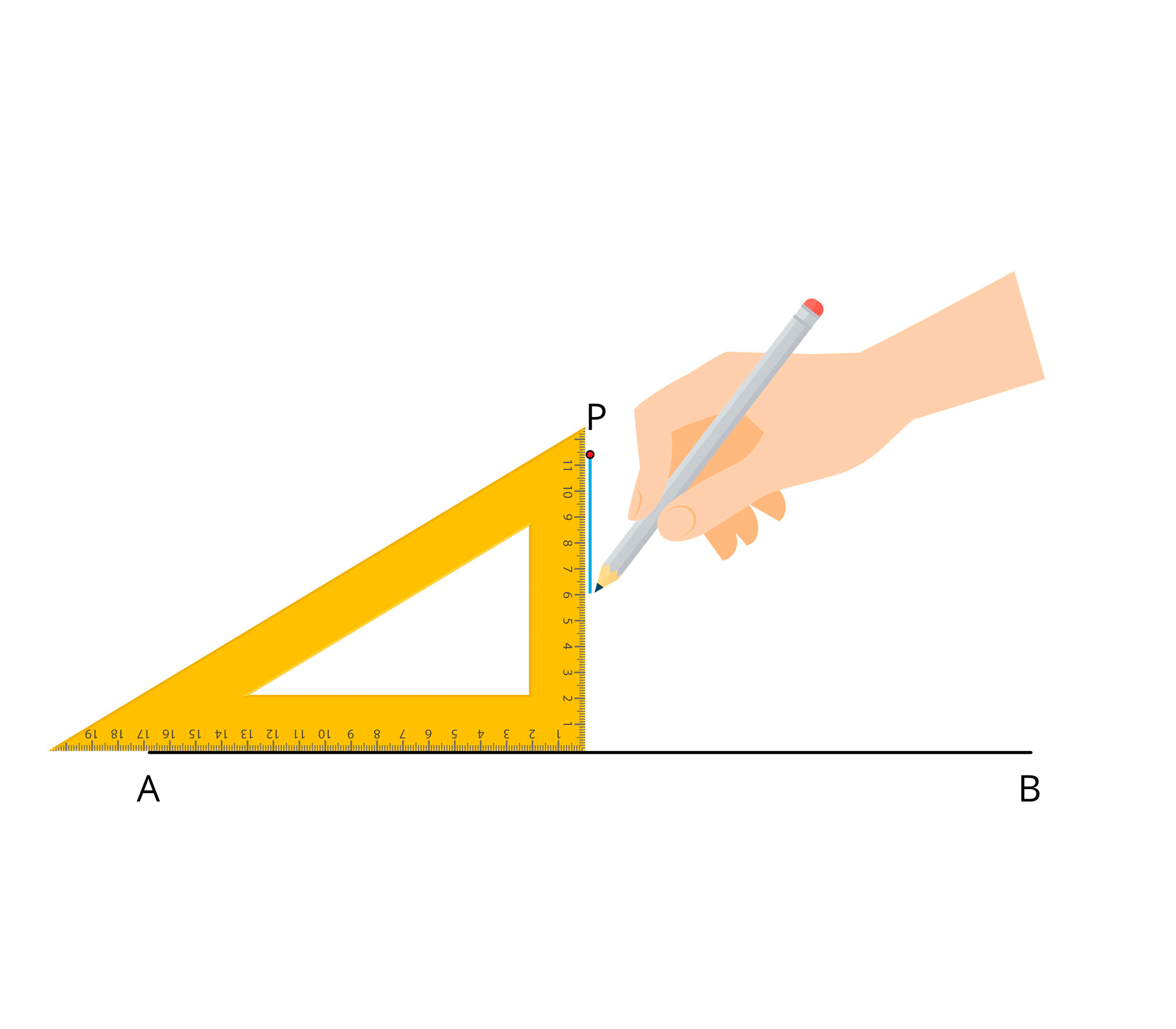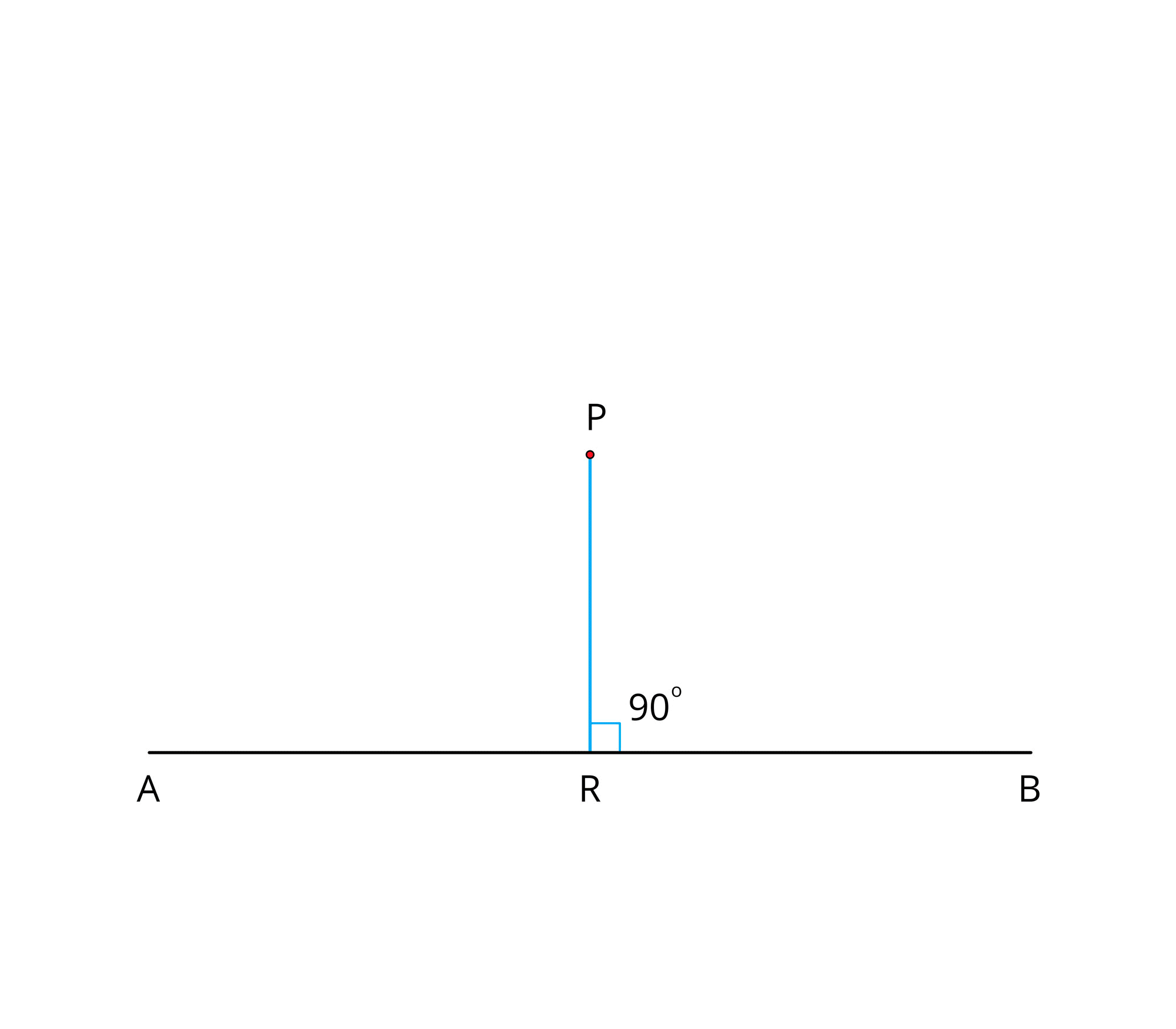
Draw a line perpendicular to the given line through a point above it.
Step \(1\): Draw a line \(AB\).
Step \(2\): Take a point \(P\) anywhere above the line \(AB\).
Step \(3\): Place one of the arms of the right angle of a set square along the line \(AB\) and the other arm of its right angle touches the point \(P\).
Step \(4\): Draw a line \(PR\) through \(P\) along the other arm of the right angle of the set square.
Step \(5\): The line \(PR\) is perpendicular to the line \(AB\) at \(R\). That is, \(PR \perp AB\) and \(\angle PRA = \angle PRB = 90°\).
Register for free to see more content