Triangle inequality for sum of two sides — lesson. Mathematics State Board, Class 6.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

In any triangle, the sum of the length of any two sides is always greater than the length of the third side.

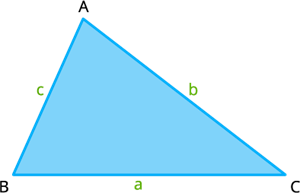
Here

$AB = c, BC = a$ and

$CA = b$ .

Thus the above inequality can be written in the notations as follows:

$a + b > c$

$b + c > a$ and

$c + a > b$ .

Example:

Consider the triangle

$ABC$ with sides measures

$AB = c = 3 cm, BC = a = 4 cm$ and

$AC = b = 5 cm$ .

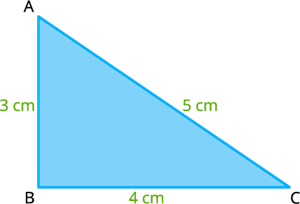
Let's check the triangle inequality for the triangle

$ABC$ ,

$a + b = 4 + 5 = 9 > 3 = c$

$b + c = 5 + 3 = 8 > 4 = a$ and

$c + a = 3 + 4 = 7 > 5 = b$ .

Did you find an error?

4. Triangle inequality for sum of two sides