PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoDid you ever wonder how computers perform calculation fast?
Computers play a vital role in day-to-day life. It has become more important in our life because it is used in very small shops to large industries. The use of computers has grown largely because of its speed, accuracy and ability to process billions of instructions in a second. And the calculation result provided by the computer will be correct, and there is no need for verifying. Computers perform all the calculations by converting them into tree diagrams.
In this topic, let us learn how to convert algebraic expression/numeric expression into tree diagram and tree diagram into numerical expression/algebraic expression.
What is a tree diagram?
Let us consider an example to understand the concept.
Consider the expression \([(6 + 2) \div 4]\) \(\times\) \(3\). Convert it into a tree diagram.
Solution:
Step \(1\): Let us name the expressions.
Let \(a_1 = b_1 \div y_1\), \(a_2 = 3\), \(b_1 = x_1 + x_2\), \(x_1 = 6\), \(x_2 = 2\), \(y_1 = 4\).
Step \(2\): Construct the diagram for the first expression.
Step \(3\): Let us first construct the diagram for \(a_1\).
Here, \(a_1 = b_1 \div y_1\) where \(b_1 = 6 + 2\) and \(y_1 = 4\).
Step \(4\): Expanding \(b_1\), we have:
\(b_1 = x_1 + x_2\) where \(x_1 = 6\), \(x_2 = 2\)
Step \(4\): Now, joining all the expressions in the diagram, we have:
Step \(5\): Now, substituting the values for the variables, we get:
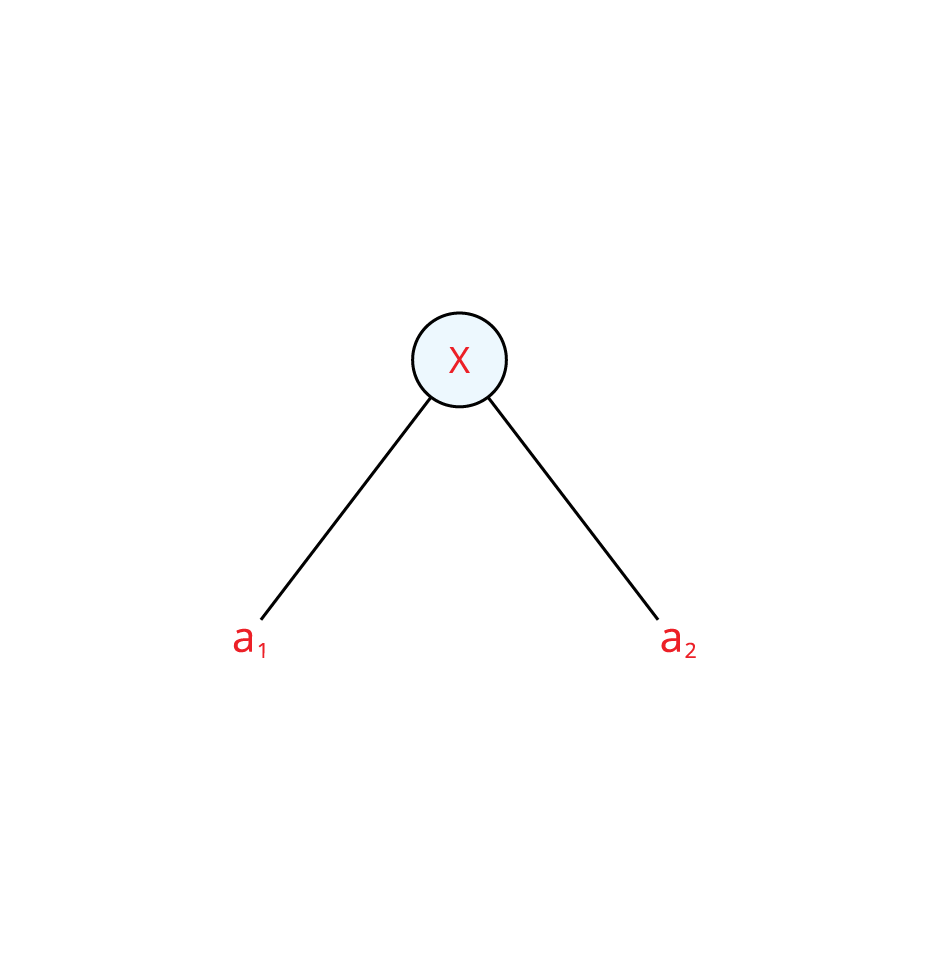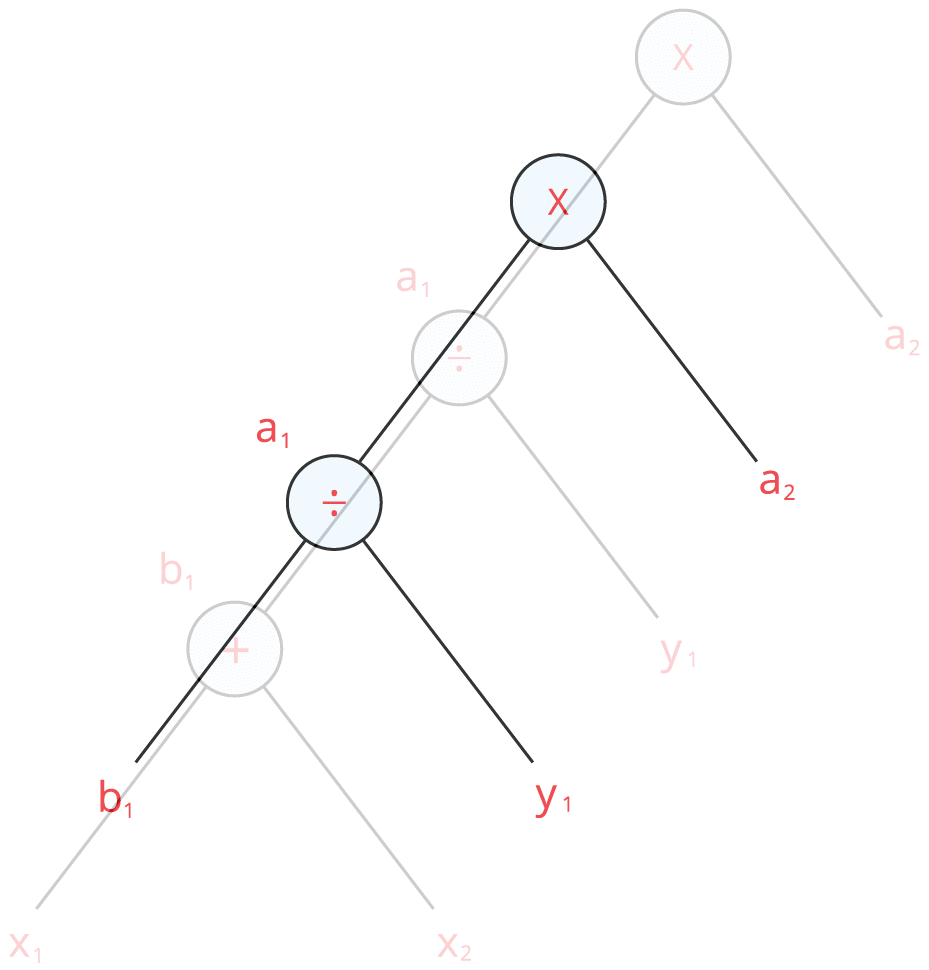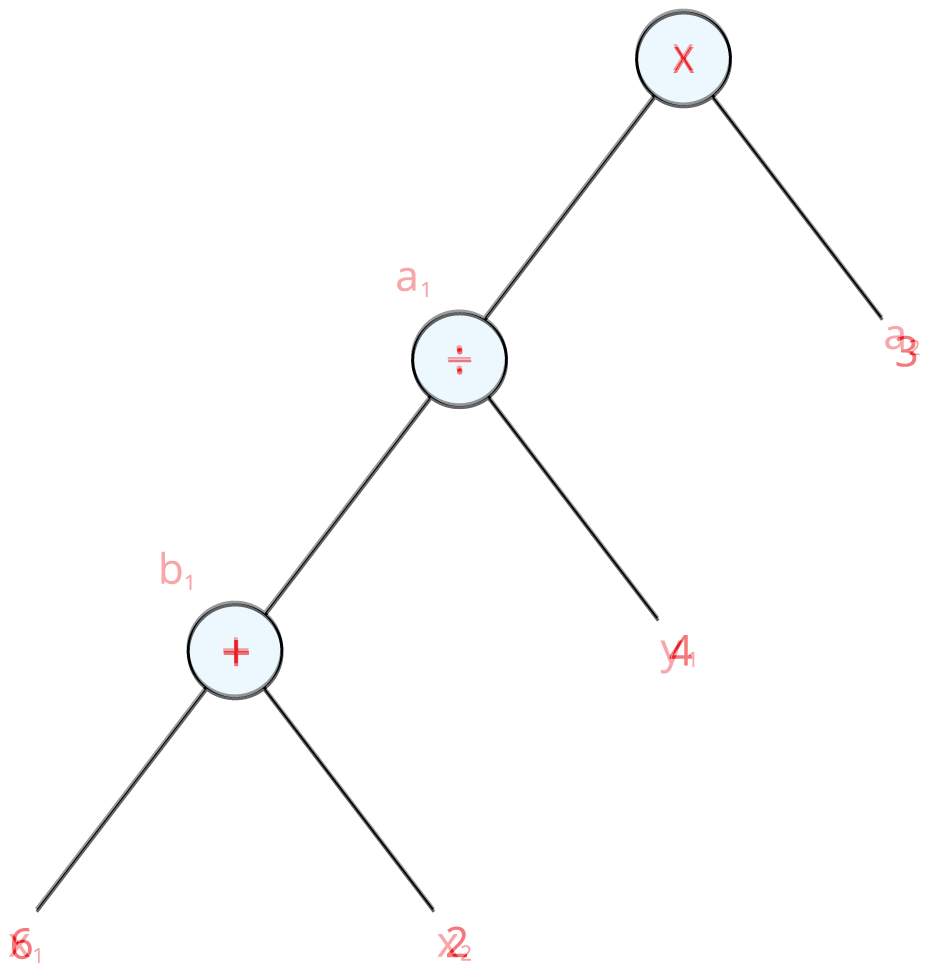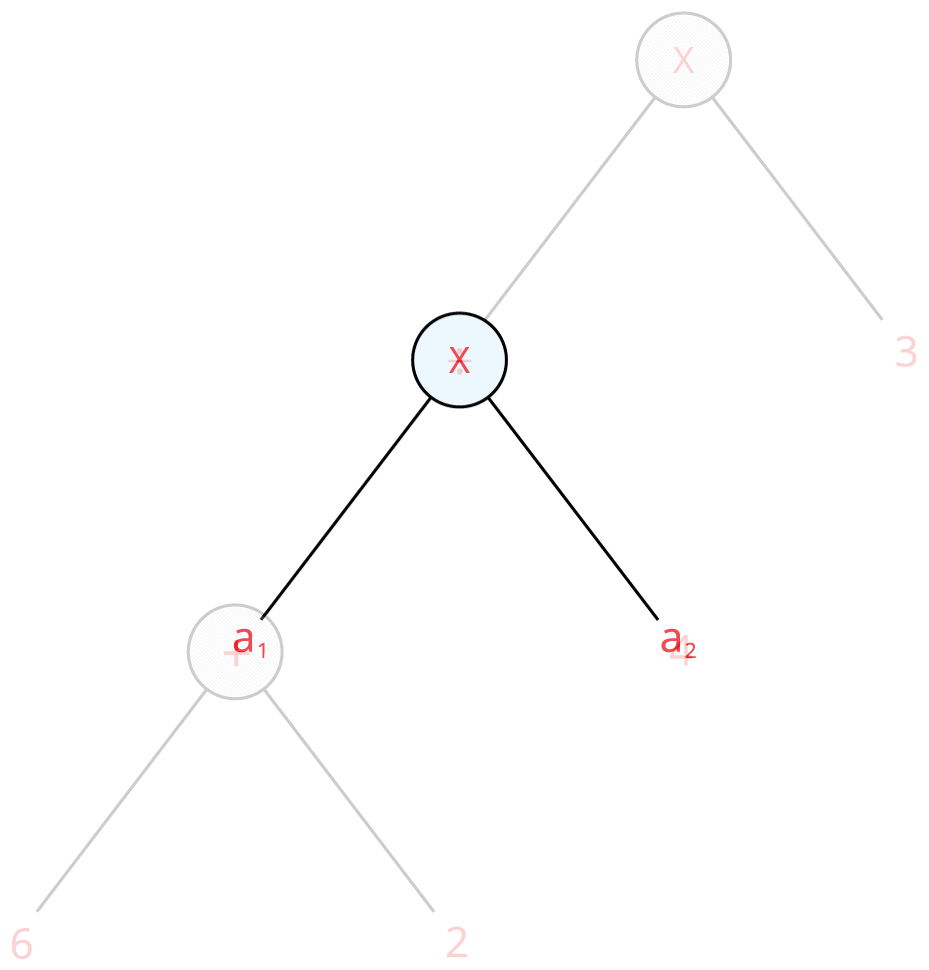
From the above diagram, we can see that each node has one or two branches, and each node has an operation in it. This diagram is called as tree diagram as it looks like a tree when we look from upside down. Here, the root is at the top and the leaves are at the bottom.
Let us consider an example to convert algebraic expressions into tree diagrams.
Convert the algebraic expression \(5a + 2b\) into a tree diagram.
Solution:
The tree diagram for the algebraic expression \(5a + 2b\) is given by:
Register for free to see more content