UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn more1. If the date of birth of Rahul is \(14/04/2005\), what is his age on \(04/02/2021\)?
Date of birth \(=\) \(12/04/2005\)
To find the age on date \(=\) \(09/02/2021\)
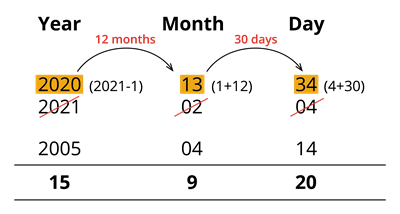
Rahul's age on date \(09/02/2021\) is \(15\) years \(9\) months \(20\) days.
2. If \(15^{\text{th}}\) of August \(2020\) is Saturday, what is the day on \(10^{\text{th}}\) January \(2021\).
Solution:
Given: \(15^{\text{th}}\) of August \(2020\) is Saturday.
Number of days in August \(=\) \(31-14 =17\)
Number of days in September \(=\) \(30\)
Number of days in October \(=\) \(31\)
Number of days in November \(=\) \(30\)
Number of days in December \(=\) \(31\)
Number of days in January \(=\) \(10- 1 = 9\)
Total number of days \(=\) \(17 + 30 + 31 + 30 + 31 + 9 = 148\)
A week has \(7\) days.
So, divide \(148\) days by \(7\) days.
\(148\) days \(=\) \(21\) weeks \(+\) \(1\) day
So, the required day is \(1\) day after Saturday.
Therefore, \(10^{\text{th}}\) January \(2021\) is Sunday.
Important!
If the remainder is:
\(0\) - Same given day
\(1\) - One day after the given day
\(2\) - Two days after the given day
\(3\) - Three days after the given day
\(4\) - Four days after the given day
\(5\) - Five days after the given day
\(6\) - Six days after the given day
Register for free to see more content