
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoThe product of the two given numbers is equal to the product of their HCF and LCM.
That is, \(\text{Product of given numbers} = \text{HCF} \times \text{LCM}\)
Example:
Find HCF and LCM of two numbers \(6\) and \(16\) and verify the relationship between them.
Solution:
HCF:
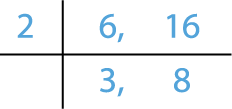
HCF of \(6\) and \(16\) \(=\) \(2\)
LCM:
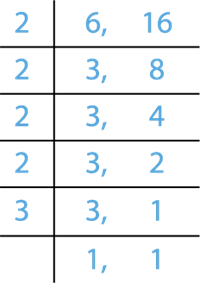
LCM of \(6\) and \(16\) \(=\) \(2 \times 2 \times 2 \times 2 \times 3 = 48\)
Relationship between HCF and LCM:
\(\text{Product of given numbers} = \text{HCF} \times \text{LCM}\)
\(6 \times 16 = 2 \times 48\)
\(96 = 96\)
Both are the same.
Hence, the relationship between LCM and HCF is verified.