
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoThe Highest Common Factor (HCF) of two or more given numbers is the largest number of their common factors. It is also called the Greatest Common Divisor (GCD).
To find the HCF of two or more numbers, we can use any of the following methods.
1. Common factor method
2. Division method
HCF by common factor method:
Let’s find the HCF of \(18\) and \(24\).
First, find all factors of the given numbers individually.
| \(1 \times 18 =18\) | \(2 \times 9 = 18\) | \(3 \times 6 = 18\) | \(18 \times 1 =18\) | \(9 \times 2 = 18\) | \(6 \times 3 = 18\) |
Factors of \(18 =\) \(1\), \(2\), \(3\), \(6\), \(9\), \(18\).
| \(1 \times 24 =24\) | \(2 \times 12 = 24\) | \(3 \times 8 = 24\) | \(4 \times 6 =24\) | \(6 \times 4 = 24\) | \(8 \times 3 = 24\) | \(12 \times 2 = 24\) | \(24 \times 1 = 24\) |
Factors of \(24 =\) \(1\), \(2\), \(3\), \(4\), \(6\), \(8\), \(12\), \(24\).
Common factors of \(18\) and \(24\) are \(1\), \(2\), \(3\) and \(6\).
Highest common factor among the above common factors is \(6\).
Therefore, HCF of \(18\) and \(24\) is \(6\).
HCF by division method:
1. Let’s find the HCF of \(27\) and \(45\).
First, we have to find the prime factors of \(27\).
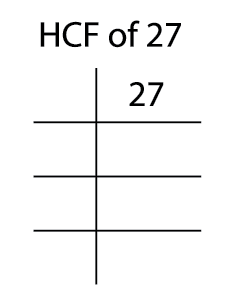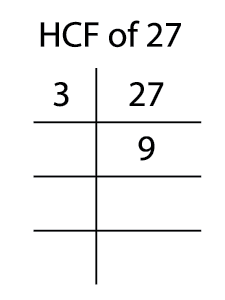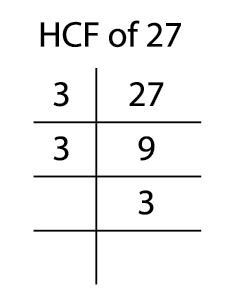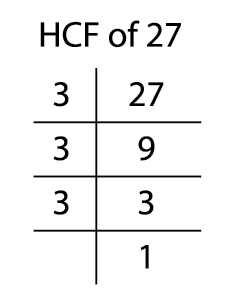
\(27=3\times3\times3\)
Now, find the prime factors of \(45\).
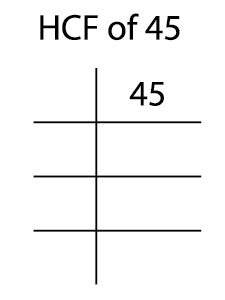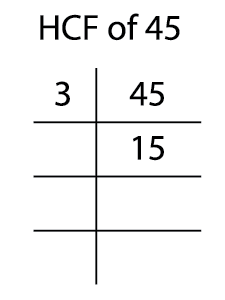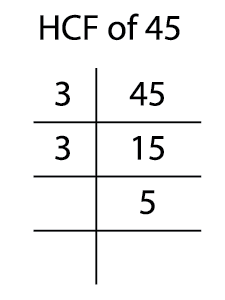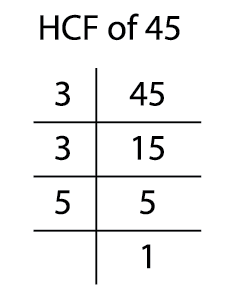
\(45 = 3 \times 3 \times 5\)
The prime factorization of \(27\) and \(45\) are:
\(27 = 3 \times 3 \times 3\)
\(45 = 3 \times 3 \times 5\)
Take the common factors of \(27\) and \(45\).
\(3 \times 3 = 9\)
Therefore, HCF of \(27\) and \(45\) is \(9\).
Let’s find the HCF by prime factorization method.
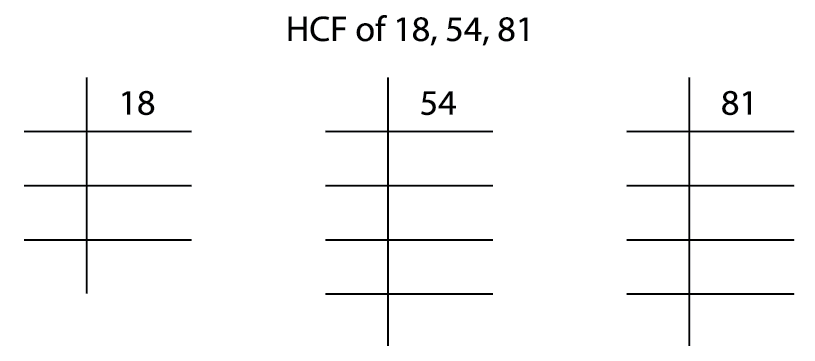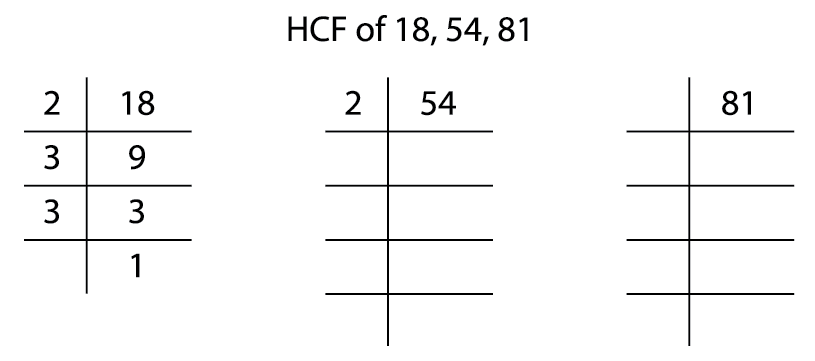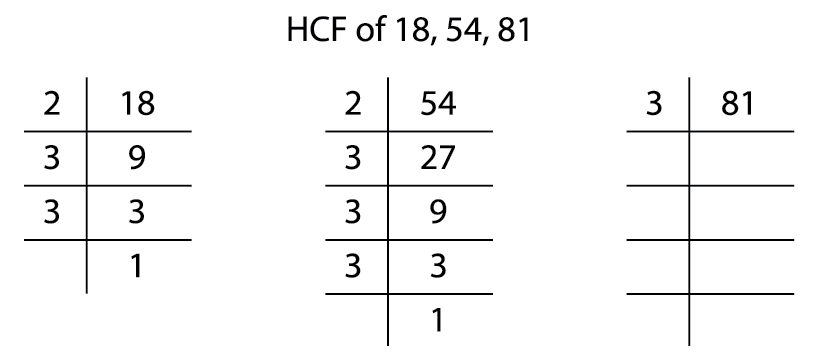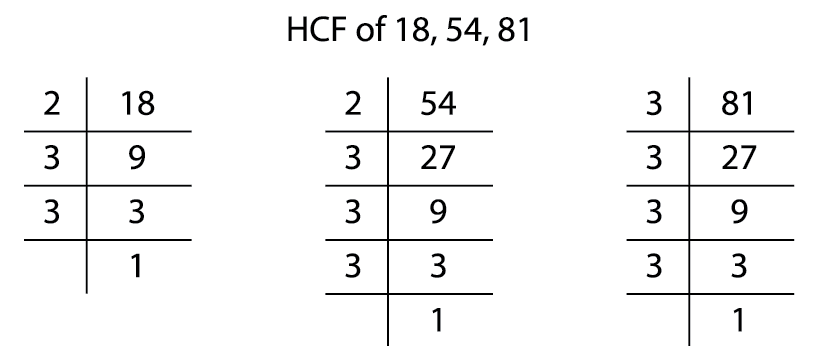
\(18 = 2 \times 3 \times 3\)
\(54 = 2 \times 3 \times 3 \times 3\)
\(81 = 3 \times 3 \times 3 \times 3\)
Take the common factors of \(18\), \(54\) and \(81\), which appear in all the three numbers.
\(3 \times 3 = 9\)
Therefore, HCF of \(18\), \(54\) and \(81\) is \(9\).