PDF chapter test TRY NOW
Eratosthenes was a Greek mathematician, astronomer, and geographer in Egypt in \(200\) B.C. He invented a method for finding prime numbers that are still used today.

Let's see how to find the prime number using the Eratosthenes sieve method:
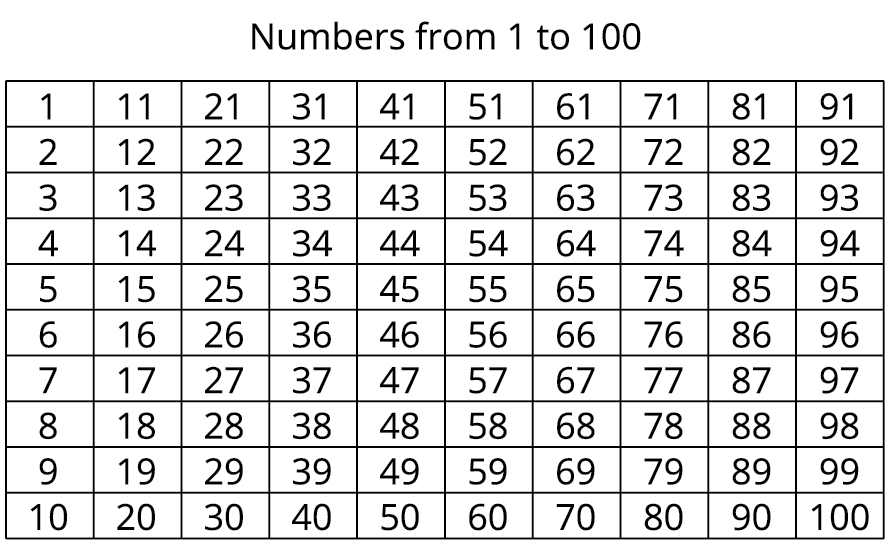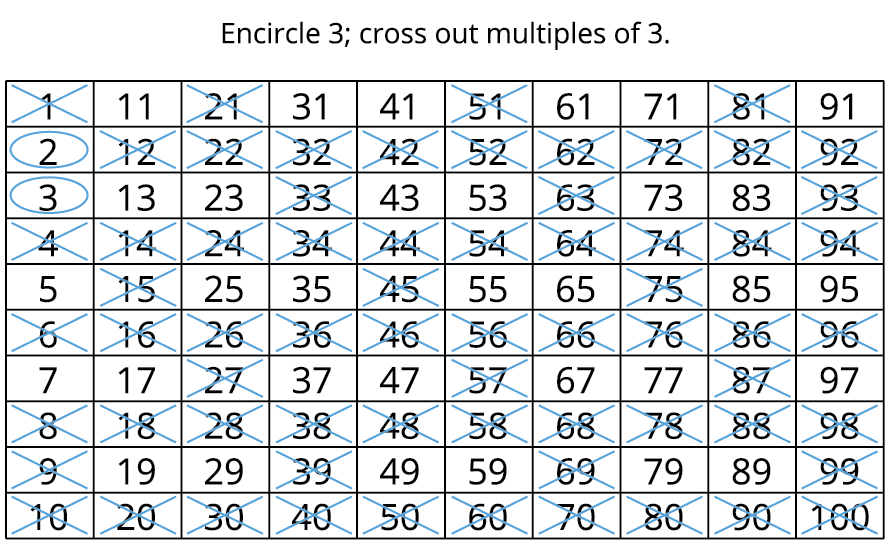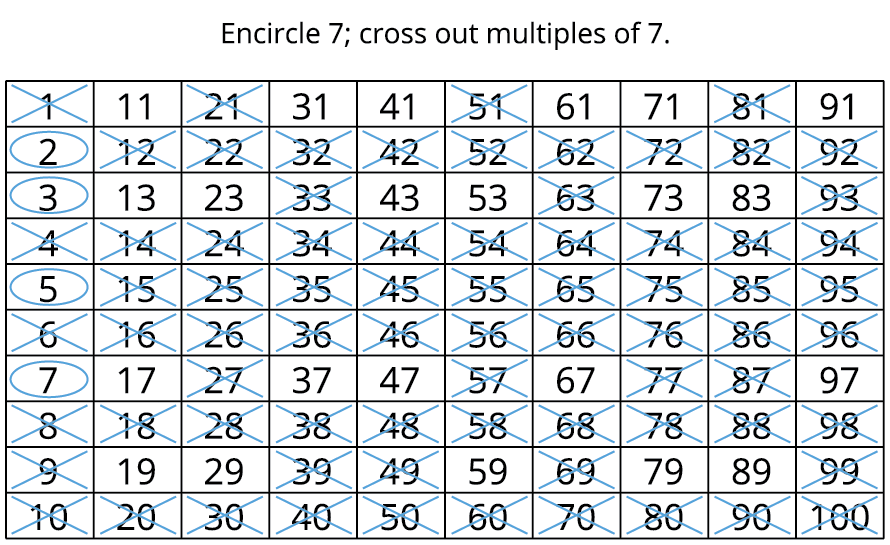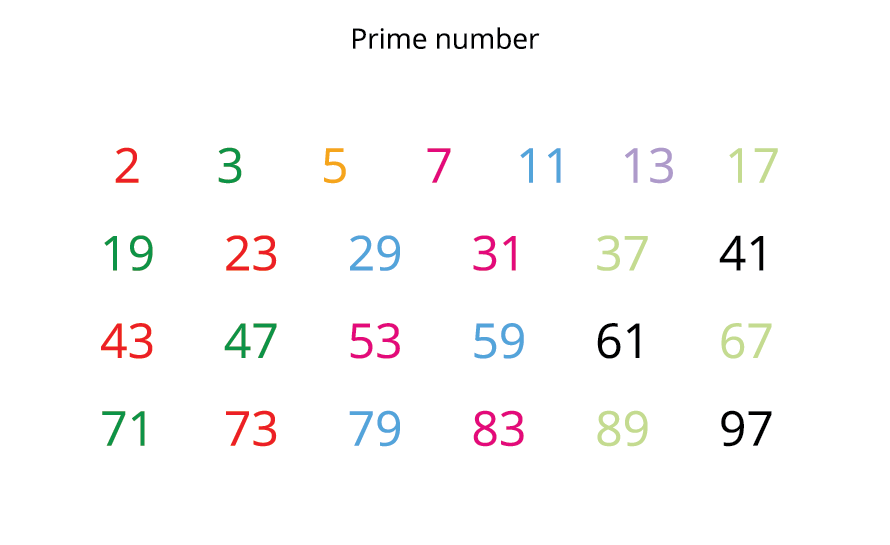
Step 1: Cross out \(1\), since it is neither prime nor a composite number.
Step 2: Encircle \(2\). All the numbers divisible by \(2\) are even numbers. So cross out all the multiples of \(2\).
Step 3: Encircle \(3\); cross out multiples of \(3\).
Step 4: Encircle \(5\); cross out multiples of \(5\).
Step 5: Encircle \(7\); cross out multiples of \(7\).
Step 6: Encircle \(11\); cross out multiples of \(11\).
Step 7: All the encircled numbers are prime numbers. Rest all the crossed-out numbers except \(1\) are composite numbers.
\(2\), \(3\), \(5\), \(7\), \(11\), \(13\), \(17\), \(19\), \(23\), \(29\), \(31\), \(37\), \(41\), \(43\), \(47\), \(53\), \(59\), \(61\), \(67\), \(71\), \(73\), \(79\), \(83\), \(89\), \(97\).
Yes! we got all prime numbers from \(1\) to \(100\).
