PDF chapter test TRY NOW
Let us first look at the following example.
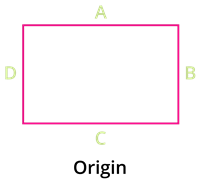
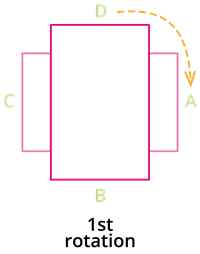
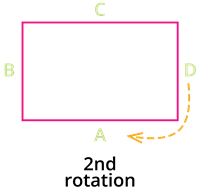
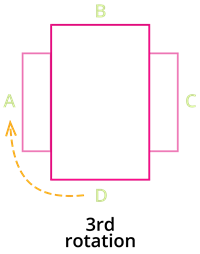
Let us analyze the example given above in detail.
1. Origin is the original position of the rectangle.
2. During the first rotation, the rectangle takes a \(90\)\(°\) shift, and it does not resemble the original position.
3. During the second rotation, the rectangle takes another \(90\)\(°\) shift. Now, the position of the rectangle resembles that of the origin's.
4. During the third rotation, the rectangle further moves for a \(90\)\(°\), and it does not resemble the original position of the rectangle.
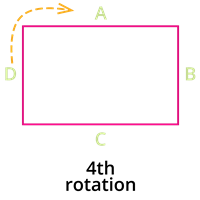
5. During the fourth and the final rotation, the rectangle takes a last \(90\)\(°\) shift, and it gets back to the original position.
[Note: To differentiate between each of the rotations, have a close look on the markings \(A\), \(B\), \(C\) and \(D\).]
Order of rotation:
When an object begins its rotation of a certain angle, the number of times it resembles the original position before it gets back to the origin marks the order of rotation.
Continuing with the previous example, we find:
The rectangle resembling the origin during the second rotation, and it gets back to the position of the origin during the fourth and final rotation.
The rectangle resembles the origin in two places.
Therefore, the order of rotation is \(2\).
Important!
A regular polygon has sides of equal lengths.
A regular polygon of '\(n\)' number of sides has '\(n\)' as order of rotation.
For instance, a square is a regular polygon and it has \(4\) sides.
Therefore, the order of rotation of a square is \(4\).
Register for free to see more content