UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreFigures with exactly two lines of symmetry:
We all know that a figure can contain two or more lines of symmetry.
Let us look at a few examples with exactly two lines of symmetry.
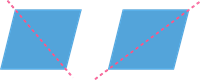
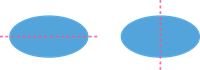
In the above example, the same shape can be cut into two identical halves in two different ways.
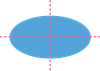
So the same shape with both the lines of symmetry will look like this.
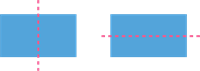
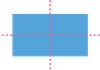
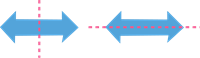
Let us also look at a few more examples with exactly two lines of symmetry.
|
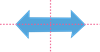
Shape
|
Lines of symmetry
|
Final figure
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
The shapes mentioned above will only have precisely two lines of symmetry. No other line can cut these shapes into identical halves.
Figures with two or more lines of symmetry:
In a few cases, there can be two or more lines of symmetry.
Consider the following figure:
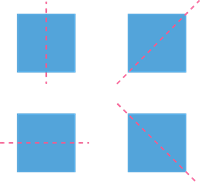
The final figure will look like this:
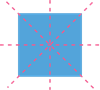
A square has four equal sides. So it is a regular polygon.
A square has \(4\) lines of symmetry.
In case of regular polygons, the number of lines of symmetry equals the number of sides.
A polygon:
If three or more line segments form a closed surface, then it is a polygon. The line segment can be of any length.
If three or more line segments of equal length form a closed surface, then it is called a regular polygon. Equilateral triangle, square, pentagon and hexagon are a few examples of regular polygon.
Let us look at a few more examples.
|
Shape
|
Number of sides
|
Lines of symmetry
|
Final figure
|
 |
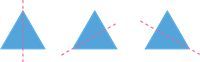
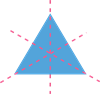
\(3\)
|
 |
 |
 |
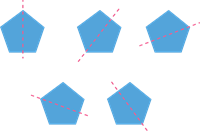
\(5\)
|
 |
 |
 |
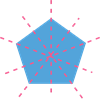\(6\)
|
 |
 |
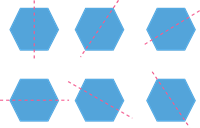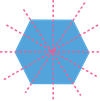Register for free to see more content