PDF chapter test TRY NOW
We might have seen the cross-section of train and track and the road while we are travelling. We can notice the corresponding angles on the intersection of tracks and road as pictured below.
If we drew just the outline of the above diagram, we get a figure as given below.
Now take a moment to observe that the pair of angles \(∠a\) and \(∠e\). These are marked at the right side of the transversal line \(l\). In that, \(∠a\) lies above the line \(m\) and \(∠e\) lies above the line \(n\).
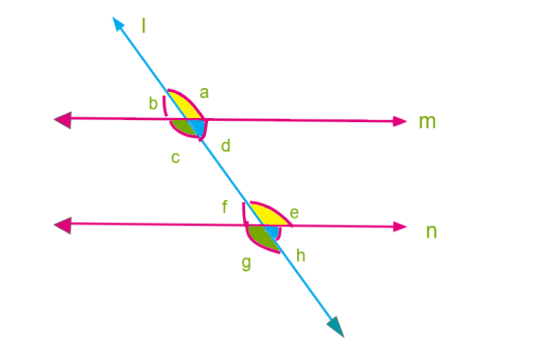
Notice that the pair of angles \(∠a\) and \(∠e\) that are marked at the right side of the transversal line \(l\). In that \(∠a\) lies above the line \(m\) and \(∠e\) lies above the line \(n\).
Also, observe the pair of angles \(∠b\) and \(∠f\) that are marked on the left of the transversal line \(l\). In that \(∠b\) lies above \(m\) and \(∠f\) lies above \(n\).
Similarly, we can see that the pair of angles \(∠c\) and \(∠g\) that are marked on left of transversal line \(l\). In that \(∠c\) lies below \(m\) and \(∠g\) lies below \(n\).
Observe the pair of angles \(∠d\) and \(∠h\) that are marked on the right of transversal line \(l\). In that \(∠d\) lies below \(m\) and \(∠h\) lies below \(n\).
So all these pairs of angles have different vertices, lie on the same side (left or right) of the transversal line \((l)\) lie above or below the lines \(m\) and \(n\). Such pairs are called corresponding angles.
Similarly, we can see that the pair of angles \(∠c\) and \(∠g\) that are marked on left of transversal line \(l\). In that \(∠c\) lies below \(m\) and \(∠g\) lies below \(n\).
Observe the pair of angles \(∠d\) and \(∠h\) that are marked on the right of transversal line \(l\). In that \(∠d\) lies below \(m\) and \(∠h\) lies below \(n\).
So all these pairs of angles have different vertices, lie on the same side (left or right) of the transversal line \((l)\) lie above or below the lines \(m\) and \(n\). Such pairs are called corresponding angles.
Each pair of corresponding angles are equal only a transversal line cuts the parallel lines.
Register for free to see more content