PDF chapter test TRY NOW
Distance:
Distance refers to the length of space between two points.
Let's consider the example given below:
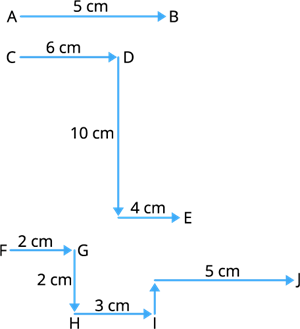
In the given image, the distance between \(A\) and \(B\) is \(5\) \(cm\). Whereas the distance between \(C\) and \(E\) has a waypoint \(D\) in the middle. Hence, we add up the distances of all the waypoints between the two points. Therefore, the distance between \(C\) and \(E\) is \(20\) \(cm\) (\(6+10+4\)) similarly, the distance between \(F\) and \(J\) is \(12\) \(cm\).
S.I Units:
S.I is an abbreviation of Système Internationale (a French word) or International System. It is the set of physical units agreed upon by international convention. The SI units are sometimes also known as MKS units, where MKS stands for "meter(for length), kilogram(for mass), and second(for time).
Conversion between millimetre, centimetre, metre and kilometre is made easier by the conversion grid given below:
As the base unit for length in the SI is metre, other length units can be related to metre as follows:
- Kilometre (\(km\)) – a thousand times bigger than a metre
- Centimetre (\(cm\)) – a hundredth of the size of a metre
- Millimetre (\(mm\)) – a thousandth of the size of a metre.
Example:
- To convert \(8 cm\) to \(m\), \(8\) has to be divided(from the conversion grid given above) by \(100\). Therefore, \(8 cm\) is \(0.08 m\).
- To convert \(12 km\) to \(mm\), \(12\) has to be multiplied with \(1000000\) (\(1000 x 100 x 10\)) therefore, \(12 km\) is \(12000000 mm\).
Register for free to see more content