UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreTo calculate the area of a trapezium, we have to multiply the sum of the parallel sides with a perpendicular distance between them and divide by \(2\).
Area of a trapezium \(A\) \(=\) (\(a + b\))\(×h\) square units.
Where \(A\) is the area of the trapezium, '\(a\)' and '\(b\)' is the length of the parallel sides, and '\(h\)' is the perpendicular distance between the parallel sides.
Let us derive the formula for the area of trapezium by splitting the trapezium into two triangles.
To prove the area of a trapezium \(A =\) (\(a + b\))\(×h\) square units.
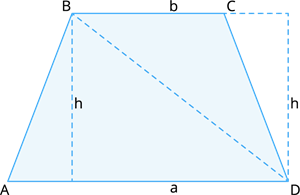
We know that, Area of trapezium \(ABCD =\) Area of \(Δ ABD\) \(+\) Area of \(ΔCBD\).
Now, find the area of \(ΔABD\) and the area of \(ΔBCD\) separately and add them to get the area of trapezium.
Area of \(ΔABD\) \(+\) Area of \(ΔCBD =\) \(b × h\) \(+\) \(b × h\).
From the above figure, the base of \(ΔABD =\) \(a\) and the base of \(ΔCBD =\) \(b\)
Also, the height of the triangles, \(ΔABD = ΔCBD = h\).
Substitute the known value.
Area of trapezium \(ABCD =\) \(b × h\) \(+ a × h\).
Taking \(h\) commonly outside gives:
\(=\) (\(a + b\))\(× h\)
Thus, the area of the trapezium \(ABCD =\) (\(a + b\))\(×h\) square units.
Register for free to see more content