2. Addition on number line

 

Take a white sheet and draw a straight line.

 

 

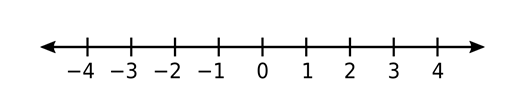
Refer to the above diagram and mark the line by numbers. The distance between all the numbers should be equal. That is the distance which is between \(0\) and \(1\) should be of the same distance for all the numbers. This distance is known as unit distance.

 

Now we know that all the numbers are separated by equal units.

 

The addition of the whole can be represented using a number line figure.

 

Now we are going to see the addition of \(2\) and \(5\).

 

 

 

1. Start from \(2\). Since we add \(5\) to this number, so we have to make \(5\) jumps to the right side of the number line;

 

2. The arrow should go like \(2\) to \(3\), \(3\) to \(4\), \(4\) to \(5\), \(5\) to \(6\) and \(6\) to \(7\), as shown in the above figure. The tip of the last arrow in the fourth jump is at \(7\).

 

Therefore we get \(2 + 5 = 7\)

 

Now using the same concept, we are going to add $(+8)+(-5)$.

  

1. To add \(+8\) and \(–5\), we should start from zero and move eight steps towards the right side of the number line (Positive integers) forward to represent \(+8\)

 

2. Since the operation is addition, we maintain the same direction and move three units backwards to represent \(–5\). Now we reached the number \(+3\), which is the result of $(+8)+(-5)=+3$.