Highest common factor — lesson. Mathematics State Board, Class 8.

PDF chapter test TRY NOW

You learned the basic concept of common factor, LCM and HCF in the previous classes. Now we remember it, and then we explore more about it.

Common factor:

When we find factors for two or more numbers, if any factors are common (same) between the numbers, they are called common factors.

Example:

Let us find the common factors of \(15\), \(45\), \(50\).

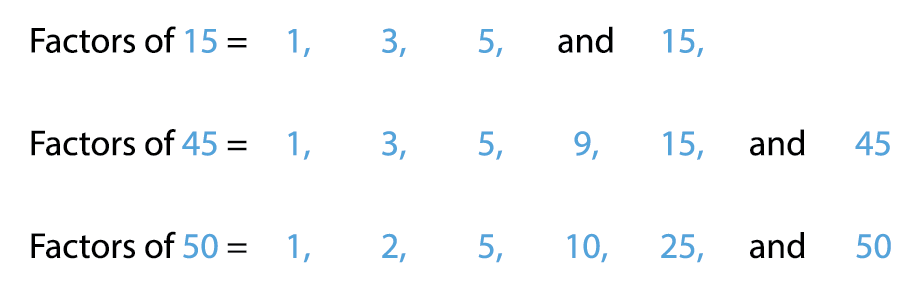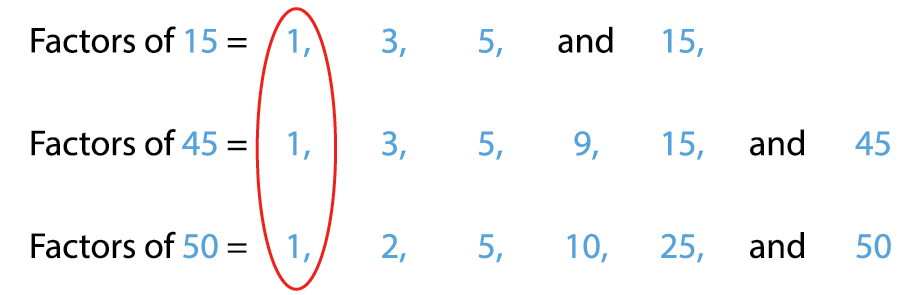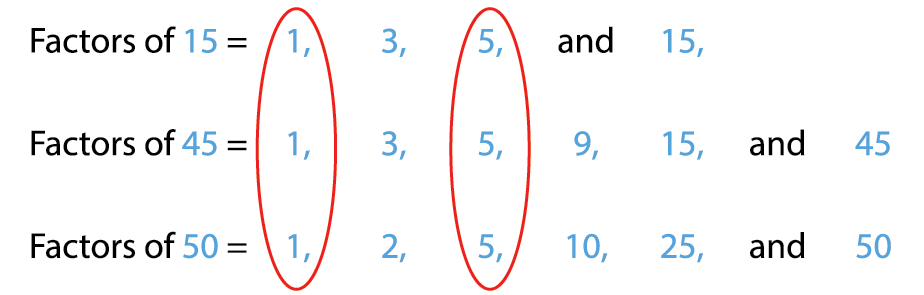
Therefore, the common factors of \(15\), \(45\), and \(50\) are \(1\) and \(5\).

Highest common factor

The Highest Common Factor (HCF) of two or more given numbers is the largest number of their common factors. It is also called the Greatest Common Divisor (GCD).

Let us see how the HCF is applied in our daily life.

Consider that Harish have 20 chocolates and 15 cake pieces, and he wants to give those together equally among friends who are visited his birthday party.

Can you help him to find how many maximum numbers of persons he can provide those equally?

Now we find the HCF of 20 chocolates and 15 cake pieces to get the answer.

Factors of 20: \(1\), \(2\), \(4\), \(5\), \(10\), \(20\)

Factors of 15: \(1\), \(3\), \(5\), \(15\).

The common factor of 20 and 15 is \(5\). So the HCF is \(5\). Therefore, for \(5\) persons, Harish can give 4 chocolates \((\)

\frac{20}{5}

\(= 4)\) and 3 cake pieces to \((\)

\frac{15}{5}

\(= 3)\).

Methods To Find HCF:

To calculate the HCF, we can use a variety of methods. However, in this section, we will look at the two most fundamental ways.

1. Repeated Subtraction Method

2. Repeated Division Method

Repeated Subtraction Method

We can apply the following step to find the HCF through the repeated subtraction method.

Step 1: To find the HCF for a given pair of numbers, say \((a)\) and \((b)\), we subtract continuously until \((a)\) and \((b)\) equal.

Step 2: When \((a)\) is greater than \((b)\), we do \((a - b)\) and allocate the result (the difference) to \((a)\). We check if \((a)\) and \((b)\) are equal again, and then repeat the procedure.

When \((a)\) is less than \(b\), we perform \((b - a)\) and assign the outcome (the difference) to the variable \((b)\). We check if \((a)\) and \((b)\) are equal again, and then repeat the procedure.

Step 3: When \((a)\) and \((b)\) are both equal, that equal number will be HCF (\((a)\), \((b)\)).

Now we apply this steps to an example to understand this well.

Example:

Find the HCF of 144 and 120.

Solution:

Step 1: Here we take \(a =\) 144 and \(b =\)120.

We should check whether \(a = b\) or \(a > b\) or \(a < b\). Here \(a > b\).

Step 2: Subtract the smaller number from the larger number till \(a = b\).

First,