PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA triangle has \(3\) sides, \(3\) vertices, and \(3\) angles. A triangle whose vertices \(A\), \(B\), and \(C\) referred to \(△ABC\).
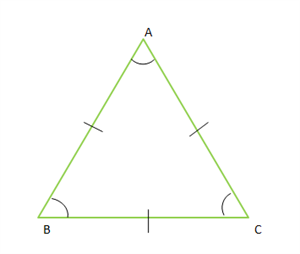
Properties of a triangle:
The first property of a triangle: \(180°\) is always the sum of the three interior angles of a triangle.
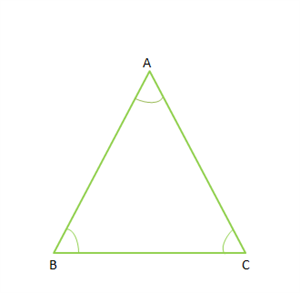
The three angles of the \(△ABC\) are \(∠A\), \(∠B\), and \(∠C\).
As per the property, the sum of the three angles of the \(△ABC\) is \(180°\).
That is, \(∠A + ∠B + ∠C = 180°\).
The second property of a triangle: The sum of the length of a triangle's two sides is always greater than the length of the triangle's third side.
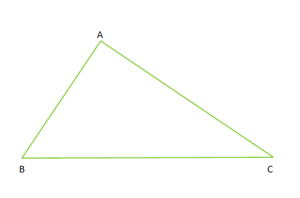
The three sides of the \(△ABC\) are \(AB\), \(BC\) and \(AC\).
As per the property, the sum of the length of any two sides of an \(△ABC\) is always greater than the length of the third side of the \(△ABC\).
Let the two sides are \(AB\) and \(BC\), and the third side is \(AC\).
Thus, we have \(AB + BC > AC\).
Similarly,
\(BC + AC > AB\) or
\(AB + AC > BC\).
Register for free to see more content