UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
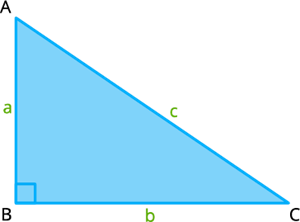
Learn moreRight angle triangle: A triangle where one of its interior angles is a right angle \(90°\).
Area:
Area(\(A\)) \(=\) \(1/2(b × h)\).
Thus, the height of the triangle(\(h\)) \(=\) Area \(× 2 / b\).
And, the base of the triangle(\(b\)) \(=\) Area \(× 2 / h\).
Where '\(h\)' is denoted as the height and '\(b\)' is denoted as the base.
Hypotenuse: The side opposite to the right angle is named the hypotenuse. It'll always be the longest side of a right triangle.
Sides: The \(2\) sides that aren't the hypotenuse makes the right angle.
Perimeter:
Perimeter(\(P\)) \(=\) \(a + b + c\).
The side length of the right triangle are in relation \(a² + b² = c²\)
Where '\(a\)', '\(b\)' are the lengths of the other two sides.
And '\(c\)' is the length of the hypotenuse.
Properties:
- If \(2\) sides which have the right angle are equal in length (\(AB\) and \(BC\)), then it said to be a right isosceles triangle.
- The hypotenuse (the side opposite the right angle) is usually longer than either of the other two sides meaning that it can never be an equilateral triangle.
Isosceles triangle: A triangle which has two of its sides equal in length.

Area:
Area(\(A\)) \(=\) \(1/2(b × h)\)
Thus, the height of the triangle(\(h\)) \(=\) Area \(× 2 / b\).
And, the base of the triangle(\(b\)) \(=\) Area \(× 2 / h\).
Where '\(h\)' is denoted as the height(altitude) and '\(b\)' is denoted as the base.
The altitude can be calculated by \(h =\) \(√( a² - b²) / 4\)
Perimeter:
In here \(a = c\), we have \((P) =\) \(a + b + c\).
Substitute the known value.
\(P =\) \(a + b + a\) \(=2a+b\)
\(P =\) \(2a+b\)
Where '\(a\)' is the lengths of the two equal sides and '\(b\)' is the lengths of the other sides.
Properties:
- The 'base' of the triangle is referred to the unequal side of an isosceles triangle.
- The base angles of an isosceles triangle are always equal. That is \(∠ABC\) \(=\) \(∠ACB\).
- The altitude is a perpendicular distance from the base to the opposite vertex.
Important!
- When the \(3rd\) angle of an isosceles triangle is a right angle, it is called a "right isosceles triangle".
- If all three sides are the same length, it is called an equilateral triangle.
- All the equilateral triangles will satisfy all the properties of an isosceles triangle.
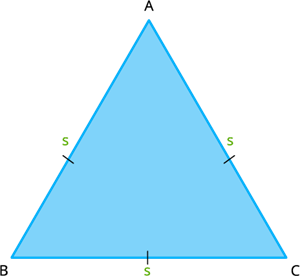
Equilateral triangle: A triangle which has all three of its sides equal in length.
Area:
Area(\(A\)) \(=\) \(√3/4 ×s²\) square units.
Where '\(s\)' denotes sides of the triangle.
Perimeter:
Perimeter(\(P\)) \(= a + b + c\) or \(P = s + s + s\).
Where '\(s\)' is the lengths of the three equal sides.
Properties:
- All three angles of an equilateral triangle are the same. Thus, the angles \(∠ABC\), \(∠CAB\) and \(∠ACB\) are always the same. Since the angles are the same and the internal angles of any triangle always add to \(180°\), each interior angle of an equilateral triangle is \(60°\).
- An equilateral triangle is one in which all three sides are congruent (same length). Because it also has the property that all three interior angles are equal.