PDF chapter test TRY NOW
Conjecture \(1\)
Illustration:
Consider a circle with centre \(O\) and a diameter \(QR\).
Place a points \(P\) on the circumference of the circle.

It is known that the angle measure of a diameter in a circle is \(180^{\circ}\).
This implies, the arc subtends an \(\angle QOR = 180^{\circ}\) at the centre \(O\) and \(\angle QPR\) at the circumference of the circle.
According to the theorem, the angle subtended by an arc of the circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
So, \(\angle QOR = 2\angle QPR\).
This implies, \(\angle QPR = \frac{1}{2} \times \angle QOR\)
\(= \frac{180^{\circ}}{2}\)
\(=\) \(90^{\circ}\)
Based on this result, we arrive at a conjecture which states:
An angle inscribed in a semi-circle is a right angle.
Explanation:

The conjecture is that any angle inscribed in the semi-circle is always \(90^{\circ}\). In other words, the angle subtended by the diameter is always \(90^{\circ}\).
Example:
Find the measure of the angle subtended by the longest chord of the circle at any point on the circumference.
Solution:
The longest chord of the circle is the diameter of the circle.
Also, the angle subtended by the diameter of the circle at any point on the circumference is the same as the angle inscribed in a semi-circle.
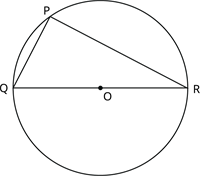
Let \(QR\) be the diameter and \(P\) be any point on the circumference.
It is known that an angle inscribed in a semi-circle is a right angle.
This implies, \(\angle QPR = 90^{\circ}\).
Therefore, the measure of the angle subtended by the longest chord of the circle at any point on the circumference is \(90^{\circ}\).
Conjecture \(2\)
Equal arcs of a circle subtend equal angles at the centre.
Explanation:
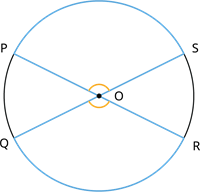
The conjecture is that if the arcs and are equal, then the angles subtended by them at the centre are equal. \(\angle POS = \angle QOR\).
Example:
If and are two equal arcs and if one of the arcs subtend an angle \(60^{\circ}\) at the centre, then find the angle measure of the other arc at the centre.
Solution:
It is known that equal arcs of a circle subtend equal angles at the centre.
Hence, it is obvious that the other arc subtends an angle \(60^{\circ}\) at the centre.
