PDF chapter test TRY NOW
Angle at the Centre and the Circumference
Illustration:
Consider a circle with centre \(O\) and place three points \(P\), \(Q\) and \(R\) on the circumference of the circle such that subtends \(\angle QOR\) at the centre \(O\) and \(\angle QPR\) at the circumference of the circle.
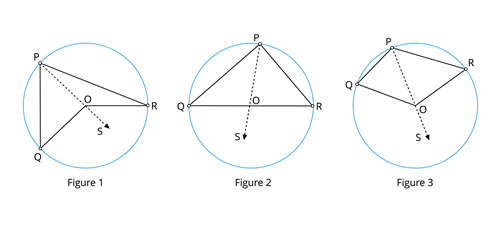
Consider three cases where (i) Figure \(1\) is minor (ii) Figure \(2\) is a semicircle and (iii) Figure \(3\) is a major arc.
In all the three cases, subtend \(\angle QOR\) at the centre and \(\angle QPR\) at the point \(P\) on the circumference of the circle.
Now let us extend \(PO\) to \(S\) and join \(PS\).
In the triangle \(POQ\), \(\angle QOS\) is an exterior angle.
By the property of the triangle, the exterior angle is equal to the sum of the interior opposite angles.
That is, \(\angle QOS\) \(=\) \(\angle OPQ\) \(+\) \(\angle PQO\).
Here, \(OP\) \(=\) \(OQ\). Since the radii are equal.
This implies that the \(\angle OPQ\) \(=\) \(\angle PQO\) as they form the base angles of the isosceles triangle \(POQ\).
Therefore, \(\angle QOS\) \(=\) \(\angle OPQ\) \(+\) \(\angle OPQ\)
\(=\) \(2 \angle OPQ\) \(……\) \(\text{equation }(1)\)
In the triangle \(POR\), \(\angle ROS\) is an exterior angle.
By the property of the triangle, the exterior angle is equal to the sum of the interior opposite angles.
That is, \(\angle ROS\) \(=\) \(\angle OPR\) \(+\) \(\angle PRO\).
Here, \(OP\) \(=\) \(OR\). Since the radii are equal.
This implies that the \(\angle OPR\) \(=\) \(\angle PRO\) as they form the base angles of the isosceles triangle \(POR\).
Therefore, \(\angle ROS\) \(=\) \(\angle OPR\) \(+\) \(\angle OPR\)
\(=\) \(2 \angle OPR\) \(……\) \(\text{equation }(2)\)
Add equation \((1)\) and \((2)\), we get:
\(\angle QOS\) \(+\) \(\angle ROS\) \(=\) \(2 \angle OPQ\) \(+\) \(2 \angle OPR\)
\(\angle QOR\) \(=\) \(2 (\angle OPQ + \angle OPR)\)
\(\angle QOR = 2\angle QPR\)
Based on this result, the following theorem is obtained.
Theorem: The angle subtended by an arc of the circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Explanation:
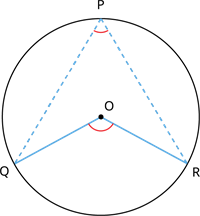
The theorem states that the angle subtended by the arc of the circle at the centre \(O\) is twice the angle subtended by the point \(P\) at any remaining part of the circle. (i.e.) \(\angle QOR = 2\angle QPR\).
Example:
Find the unknown angle \(x\) in the given figure if the angle subtended by the arc at the centre \(O\) is \(160^{\circ}\).
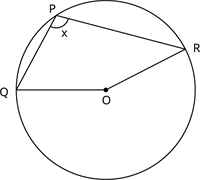
Solution:
By the theorem, \(\angle QOR = 2\angle QPR\).
This implies, \(\angle QPR = \frac{1}{2} \times \angle QOR\)
\(x = \frac{160^{\circ}}{2}\)
\(=\) \(80^{\circ}\)
Therefore, the unknown angle \(x\) is \(80^{\circ}\).
