UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn morePerpendicular from the Centre to a Chord
Illustration:
Consider a circle with centre \(O\) and a chord \(PQ\) as follows:
Draw a line \(OR\) perpendicular to the chord \(PQ\).
Join the points \(OP\) and \(OQ\).
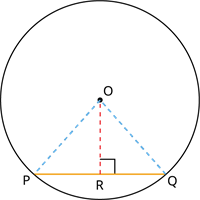
Two right triangles \(ORP\) and \(ORQ\), are obtained where \(\angle ORP = \angle ORQ = 90^{\circ}\) since \(OR \perp PQ\).
Here, \(OP\) and \(OQ\) are radius. So, they are equal.
Also, the side \(OR\) is common to the triangle \(ORP\) and \(ORQ\).
Therefore, by the RHS rule (In two right-angled triangles, if the length of the hypotenuse and one side of one triangle is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent), the triangles are congruent.
This implies that the sides \(PR = RQ\).
Based on this congruency, the following theorems are obtained.
Theorem: The perpendicular from the centre of a circle to a chord bisects the chord.
Explanation:
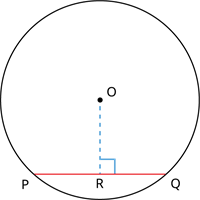
The theorem states that if \(O\) is the centre and \(PQ\) is the chord, then the perpendicular \(OR\) from the centre \(O\) to the chord \(PQ\) bisects the chord \(PQ\) (i.e.) \(PR = RQ\).
Example:
The chord of length \(24 cm\) is drawn from a perpendicular distance of \(9 cm\) from the centre of the circle. Find the radius of the circle.
Solution:
The pictorial representation of the given question is as follows:
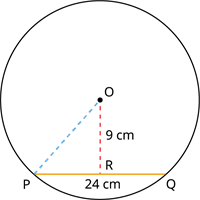
Given the distance from the centre of the circle \(=\) \(9 cm\)
The length of the chord \(=\) \(24 cm\).
Here, \(\angle ORP = 90^{\circ}\).
Therefore, by the theorem, we have:
\(PR = RQ\)
\(=\)
\(=\) 12 \(cm\)
Consider the triangle \(OPR\):
By the known Pythagoras theorem:
\(\text{Hypotenuse side}^{2} = \text{Adjacent side}^{2} + \text{Opposite side}^{2}\)
Let's find the length of \(OP\) as follows:
\(OP^{2} = OR^{2} + RP^{2}\)
\(= 9^{2} + 12^{2}\)
\(= 81 + 144\)
\(= 225\)
Thus, \(OP = \sqrt{225}\)
\(= 15\) \(cm\)
Therefore, the radius of the circle is \(15\) \(cm\).
Converse of the theorem: The line joining the centre of the circle and the midpoint of a chord is perpendicular to the chord.
Explanation:

The theorem states that if \(O\) is the centre and \(R\) is the mid-point of the chord \(PQ\), the line joining the centre \(O\) and the mid-point \(R\) is perpendicular to the chord \(PQ\).
Example:
Find the measure of the angle between the line joining the centre of the circle and the mid-point of the chord of the circle.
Solution:
By the theorem, the line joining the centre of the circle and the midpoint of a chord is perpendicular to the chord.
So, the line from the centre of the circle and the midpoint of a chord are perpendicular to each other.
That is, the angle between the line from the centre to the chord is \(90^{\circ}\).
Therefore, the measure of the angle between the line joining the centre of the circle and the mid-point of the chord of the circle is \(90^{\circ}\).