PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAngle Subtended by Chord at the Centre
Illustration:
Consider a circle with centre \(O\) and two chords \(PQ\) and \(RS\) of equal length.
Join the endpoints of the chords \(PQ\) and \(RS\) with the centre \(O\).
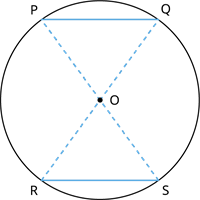
Two triangles \(OPQ\) and \(ORS\) are obtained with equal sides \(PQ\) and \(RS\) (Since the chords are equal).
The other two sides of each triangle are equal as they form the radius of the circle.
Thus, by SSS (Side-Side-Side) rule, the triangles \(OPQ\) and \(ORS\) are congruent.
Since the triangles are congruent, the angles subtended by the triangles are also equal.
Based on this congruency, the following theorem is obtained.
Theorem: Equal chords of a circle subtend equal angles at the centre.
Explanation:
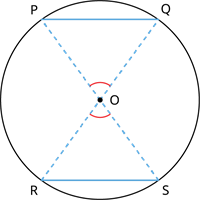
The theorem states that if the chords \(PQ\) and \(RS\) are equal, then the angle subtended by the chords respectively at the centre \(O\) are equal (i.e.) \(\angle POQ = \angle ROS\).
Example:
Find the unknown angle \(x\) in the given figure where the chords \(PQ\) and \(RS\) are equal, and \(O\) is the centre of the circle.
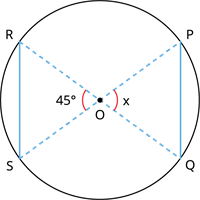
Solution:
By the above theorem, the chords \(PQ\) and \(RS\) subtend equal angle at \(O\).
This implies that, \(\angle POQ = \angle ROS\).
Here, \(\angle ROS = 45^{\circ}\).
Thus, \(\angle POQ = 45^{\circ}\).
Therefore, the unknown angle \(x = 45^{\circ}\).
Illustration:
Following the above theorem, let us find the length of the chords which subtend equal angle at the centre.
Consider a circle with centre \(O\) and two chords \(PQ\) and \(RS\).
Join the endpoints of the chords \(PQ\) and \(RS\) with the centre \(O\).
From the theorem, we have \(\angle POQ = \angle ROS\).
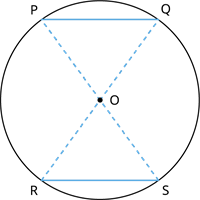
Two triangles \(OPQ\) and \(ORS\) are obtained with two sides of each triangle being equal as they form the radius of the circle.
Thus, by SAS (Side-Angle-Side) rule, the triangles \(OPQ\) and \(ORS\) are congruent.
Based on this congruency, the following theorem is obtained.
Converse of Theorem: If the angles subtended by two chords at the centre of a circle are equal, then the chords are equal.
Explanation:
The theorem states that, if \(PQ\) and \(RS\) are two chords subtending equal angle at the centre \(O\) then the chords \(PQ\) and \(RS\) equal (i.e.) \(PQ = RS\).
Example:
If two parallel chords subtend an equal angle at the centre, then prove that the chords are equal.
Solution:
Given that, the angle subtended by the two chords at the centre are equal.
According to the theorem, if the angles subtended by two chords at the centre of a circle are equal, then the chords are equal.
Therefore, the two parallel chords are equal.
Hence, proved.
Register for free to see more content