PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoTheorem I: In a parallelogram, opposite sides are equal.
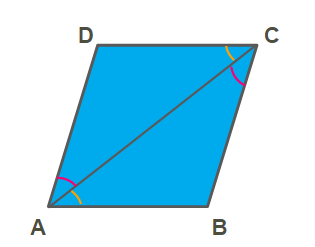
Given: A parallelogram \(ABCD\) with \(AC\) as its diagonal.
To prove: \(\Delta ABC\cong\Delta ADC\).
Proof: We know that 'Opposite sides of a parallelogram are parallel'. So, \(AB||DC\) and \(AD||BC\).
Since \(AB||DC\) & \(AC\) is the transversal.
\(∠BAC =∠DCA\) (Alternate angle ...1(yellow)).
Since \(AD||BC\) & \(AC\) is the transversal.
\(∠DAC =∠BCA\) (Alternate angle ...2(red)).
In \(△ABC\) & \(△ ADC\).
\(∠BAC =∠DCA\) (From alternate angle ...1).
\(∠DAC =∠BCA\) (From alternate angle ...2).
\(AC=AC\) (common in both).
Thus, by the \(ASA\) criterion, the two triangles are congruent, which means that the corresponding sides must be equal.
Hence, \(AB=CD\) & \(AD=BC\) (corresponding parts of congruent triangles).
Hence, it is proved.
Theorem II: A diagonal of a parallelogram divides it into two congruent triangles.
Given: A parallelogram \(ABCD\) with \(AC\) as its diagonal.
To prove: \(ΔABC ≅ ΔADC\).
Proof: We know that 'Opposite sides of a parallelogram is parallel'. So, \(AB||DC\) and \(AD||BC\).
Since \(AB||DC\) & \(AC\) is the transversal.
\(∠BAC =∠DCA\) (Alternate angle ...1(yellow)).
Since \(AD||DC\) & \(AC\) is the transversal.
\(∠DAC =∠BCA\) (Alternate angle ...2(red)).
In \(△ABC\) & \(△ ADC\).
\(∠BAC =∠DCA\) (From alternate angle ...1).
\(∠DAC =∠BCA\) (From alternate angle ...2).
From the above figure, we can write as follows:
\(∠BAC +∠BCA\) \(=\) \(∠DAC + ∠DCA\)…(1)
Apply angle sum property to the triangle \(ABC\).
\(∠B+∠BAC+∠BCA =180°\)…(2)
Now apply angle sum property to the triangle \(ACD\).
\(∠D+∠DAC+∠DCA=180°\)…(3)
Comparing (2) and (3) with (1) we have:
\(∠B = ∠D\).
From the theorem I, \(AB=CD\) & \(AD=BC\).
Thus, by the \(SAS\) criterion, the two triangles \(ABC\) and \(ADC\) are congruent, which means that the corresponding sides must be equal.
Hence, it is proved.
Register for free to see more content