
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoTheorem III: In parallelogram, opposite angles are equal.
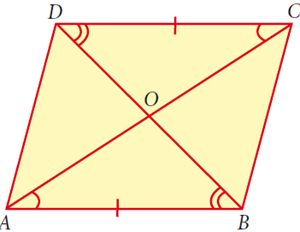
Given: A parallelogram \(ABCD\) with \(AC\) and \(BD\) as its diagonals.
To prove: \(∠A = ∠C\) & \(∠B = ∠D\).
Proof: We know that 'Opposite sides of a parallelogram is parallel and equal'. So, \(AB||DC\) and \(AD||BC\).
Since \(AB||DC\) with its transversal line \(AC\).
\(∠ACD = ∠CAB\).
Since \(AD||BC\) with its transversal line \(AC\).
\(∠DAC = ∠BCA\).
Thus, \(∠A = ∠DAC+∠CAB = ∠BCA+∠ACD = ∠C\).
Since \(AB||DC\) with its transversal line \(BD\).
\(∠CDB = ∠DBA\).
Since \(AD||BC\) with its transversal line \(BD\).
\(∠ADB = ∠DBC\).
Thus, \(∠B = DBA+∠DBC = ∠CDB+∠ADB = ∠D\).
Hence, it is proved.
Theorem IV: The diagonal of a parallelogram bisect each other.

Given: A parallelogram \(ABCD\) with \(AC\) and \(BD\) and \(O\) is the point of intesection of \(AC\) and \(BD\).
To prove: \(OA = OC\) and \(OB = OD\).
Proof: Since 'Opposite sides of a parallelogram is parallel'. So, \(AB||DC\) \(AD||BC\).
Since \(AB||DC\) & \(AC\) is the transversal.
\(∠ACD = ∠OCD = ∠CAB = ∠OAB\) (Alternate Interior angle ...1)
That is \(∠OCD = ∠OAB\).
Since \(AB||DC\) & \(BD\) is the transversal.
\(∠BDC = ∠ODC = ∠DBA = ∠OBA\) (Alternate Interior angle ...1)
That is \(∠ODC = ∠OBA\).
In \(\Delta AOB\) & \(\Delta COD\), two corresponding angles are equal (\(∠OCD = ∠OAB\) and \(∠ODC = ∠OBA\)) and a side is equal in measure.
So, \(OA = OC\) and \(OB = OD\) (Corresponding parts of Congruent triangles)
Hence, it is proved.
Theorem V: Parallelograms on the same base and between the same parallels are equal in area.
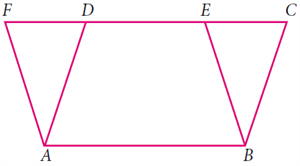
Given: Two parallelogram \(ABCD\) & \(ABEF\) that has same base \(AB\) & lies between same parallel \(CF\) & \(AB\).
To prove: Area of parallelogram \(ABCD\) \(=\) Area of parallelogram \(ABEF\)
Proof: It can be seen that the parallelogram \(ABCD\) and \(ABEF\) are on the common base \(AB\).
Here we have a pair of triangle \(ADF\) and \(BCE\).
\(\angle ADF = \angle BCD\) and \(\angle AFD \angle BEC\).
We know that \(AD = BC\) and \(AF =BE\) (Opposite sides are equal in measure).
Thus, two of the sides and two of the angles are equal.
By AAS congruence, the triangles \(ADF\) and \(BCE\) are congruent triangles.
We know that the congruent triangles have the same area.
Now, area of parllelogram \(ABCD\) \(=\) Area of \(\Delta BCE\) \(+\) Area of quadrilateral \(ABED\).
\(=\) \(\Delta BCE\)\(+\) Area of parallelogram \(ABED\)
\(=\) Area of parallelogram \(ABEF\)
Area of parllelogram \(ABCD\) \(=\) Area of parallelogram \(EFCD\)
Hence, it is proved.
In this process, we have also proved other interesting statements. These are called Corollaries, which do not need separate detailed proofs.
Important!
Corollary 1: Triangles on the same base and between the same parallels are equal in area.
Corollary 2: A rectangle and a parallelogram on the same base and between the same parallels are equal in area.