UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreScientific notation
The representation of a very large number or a very small number into a decimal form is called as scientific notation. It can be expressed as \(N = a \times 10^n\) where \(1 \leq a <10\) and \(n\) is an integer.
We have learnt that the speed of the light is \(1,08,00,00,000 \ km/hr\). We may find this a bit difficult to count the number of zeros. So, the number \(1,08,00,00,000 \ km/hr\) can be written as \(1.08 \times 10^9\) in the form of decimal number for our convenience. This form of representation is called as scientific notation.
Writing a number in scientific notation
Let us learn how to write the number in scientific notation using the following steps:
1. The decimal point is shifted to the left side of the number such that there is only one non zero number is present in the left.
2. Count the remaining digits present in the old number and write the digits to the power of \(10\).
3. If the decimal point is shifted to the left side of the number, then the power is positive. If the decimal point is shifted to the right side of the number, then the power is negative.
Example:
Convert the following into scientific notation: (i) \(2839507233\) (ii) \(0.00003794\)
Solution:
(i) Let us shift the decimal point to the left side of the number. Thus, we have:
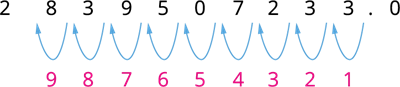
The point is moved \(9\) digits to the left. Therefore, the scientific notation is \(2.839507233 \times 10^9\).
(ii) Let us shift the decimal point to the right side of the number. Thus, we have:
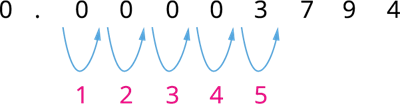
The point is moved \(5\) digits to the right. Therefore, the scientific notation is \(3.794 \times 10^{-5}\).
Consider the examples.
| Decimal notation | Scientific notation |
| \(1,000\) | \(1 \times 10^3\) |
| \(10,000\) | \(1 \times 10^4\) |
| \(10,00,000\) | \(1 \times 10^6\) |
| \(1,00,00,000\) | \(1 \times 10^7\) |
| \(0.001\) | \(1 \times 10^{-3}\) |
| \(0.00001\) | \(1 \times 10^{-5}\) |
| \(0.000001\) | \(1 \times 10^{-6}\) |
| \(0.0000001\) | \(1 \times 10^{-7}\) |
| \(0.00000001\) | \(1 \times 10^{-8}\) |
Register for free to see more content