PDF chapter test TRY NOW
While, addition or subtraction of \(2\) integers, depending upon the sign of the two or more integers, the answer can change.
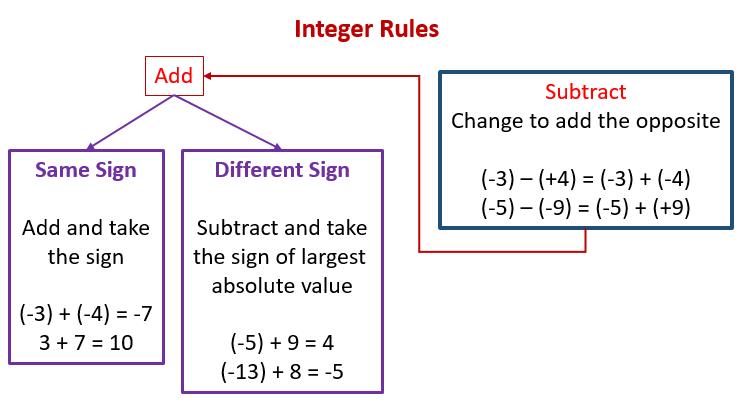
When two integers have the same sign, the sign of the answer will be the same sign of the integers.
Example:
1. In the above example, (\(-3\)) and (\(-4\)) are added both the integers have -ve sign, hence answer is \(-7\).
2. \((-6) + (-5) = -11\)
3. \(10 + 12 = 22\)
4. \((-32) + (-14) = -48\)
5. \(90 + 10 = 100\)
When two integers have a different sign, the sign of the answer will be the sign of the largest integer and both numbers will be subtracted.
Example:
1. In the above example (\(-5\)) and (\(9\)), the difference of the numbers are taken, and the sign of answer is \(+ve\). Hence the answer is\(+4\).
2. \((-20) + 13 = -7\)
3. \(30 - 15 = 15\)
4. \(20 + (-10) = 10\)
5. \(-30 + 50 = 20\)
When two integers are subtracted, (\(+ve\))\(-\)(\(-ve\)), or (\(-ve\))\(-\)(\(-ve\)), since \(-ve\) multiplied by \(-ve\) is \(+ve\), the operand between both numbers will be taken as \(+\).
Example:
1. \((-10) - (-10) = (-10) + 10 = 0\)
2. \((20) - (-10) = 20 + 10 = 30\)
3. \((-50) - (-15) = -50 + 15 = -35\)
4. \((25) - (-15) = 25 + 15 = 40\)
When two integers are subtracted, in this manner, (\(+ve\)) \(-\) (\(+ve\)), both integers should be subtracted, and the sign of the answer will be the sign of the highest integer.
Example:
1. \(30 - 10 = 20\)
2. \(40 - 12 = 28\)
3. \(10 - 50 = -40\)
4. \(20 - 48 = -28\)
