Resistances in parallel — lesson. Science CBSE, Class 10.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Parallel circuits:

Components in parallel circuits are connected to the source in two or more loops. There are multiple paths for the electric charge to flow in a parallel circuit.

Even if the circuit is broken at any point in the loop, the current can flow through the circuit. Any electric appliances linked to the circuit will also function. Hence, the electrical wiring in our houses is made of parallel circuits.

Important!

The sum of the individual currents in each parallel branch in a parallel circuit equals the main current flowing into or out of the parallel branches. The potential difference across separate parallel branches are the same.

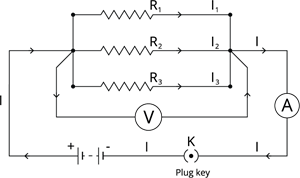
Resistors connected in parallel

Let the resistances of three resistors be \(R_1\), \(R_2\) and \(R_3\), connected parallel across points \(A\) and \(B\). Let '\(I\)' be the current flowing through the circuit.

The potential difference across the three resistances are the same and equal to the potential difference between points \(A\) and \(B\). The key is plugged, and the potential difference is measured using the voltmeter.

The current \(I\) starts from the positive terminal of the battery and reaches point \(A\). Here, the current is measured using an ammeter.

Then, the key is removed, and the ammeter and voltmeter are disconnected. Now, the ammeter is linked across the ends of the first resistor, and the current \(I_1\) is measured. Likewise, the ammeter is linked separately for the second and the third resistors, and the current \(I_2\) and \(I_3\) are found, respectively.

The current passing through the resistors \(R_1\), \(R_2\) and \(R_3\) is divided into three branches \(I_1\), \(I_2\) and \(I_3\), respectively.

According to Ohm's law, the current \(I_1\), \(I_2\) and \(I_3\) are given as,

\begin{array}{l} I_{1} = \frac{V}{R_{1}} \\ I_{2} = \frac{V}{R_{2}} \\ I_{3} = \frac{V}{R_{3}} \end{array}

Then, the total current passing through the circuit is

I = I_{1} + I_{2} + I_{3}

Substituting the values of \(I_1\), \(I_2\) and \(I_3\) in the above equation, we get

I = \frac{V}{R_{1}} + \frac{V}{R_{2}} + \frac{V}{R_{3}}

---- (eq. 1)

Let \(R_P\) be the effective resistance of the parallel combination of resistors in the circuit. Then, the (eq. 1) becomes

I = \frac{V}{R_{P}}

---- (eq. 2)

On combining (eq. 1) and (eq. 2), we get

\begin{array}{l} \frac{V}{R_{P}} = \frac{V}{R_{1}} + \frac{V}{R_{2}} + \frac{V}{R_{3}} \\ \frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \end{array}

Important!

Hence, the sum of the reciprocals of the individual resistances is equal to the reciprocal of the effective or equivalent resistance when several resistors are connected in parallel.

The effective or equivalent resistance is

\frac{R}{n}

when the '\(n\)' number of resistors having an equal resistances '\(R\)' are connected in parallel.

The above statement can be given in the form of an equation as,

\begin{array}{l} \frac{1}{R_{P}} = \frac{1}{R} + \frac{1}{R} + \frac{1}{R} + ..... + \frac{1}{R} \\ \frac{1}{R_{P}} = \frac{n}{R} \\ R_{P} = \frac{R}{n} \end{array}

Important!

The equivalent resistance in a parallel combination is less than the lowest of the individual resistances.

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

17. Resistances in parallel

Theory: