Combination of series and parallel connections — lesson. Science CBSE, Class 10.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Series connection of parallel resistors:

A series-parallel circuit is formed by connecting a set of parallel resistors in series.

Connect \(R_1\) and \(R_2\) in parallel to obtain an effective resistance of \(R_{P1}\)
Similarly, connect \(R_3\) and \(R_4\) in parallel to get an effective resistance of \(R_{P2}\)
These parallel segments of resistors are then joined in series.

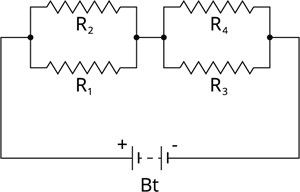
Series-parallel combination of resistors

The formula for the effective resistance of the parallel combination of resistors is,

\frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}

For two resistors in the circuit, the effective resistance is given as,

\begin{array}{l} \frac{1}{R_{P1}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ \frac{1}{R_{P2}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} \end{array}

Using the effective resistance of the series circuit,

R_{S} = R_{1} + R_{2} + R_{3}

, the net effective resistance of the series-parallel combination of resistors is,

R_{Total} = R_{P1} + R_{P2}

Parallel connection of series resistors:

A parallel-series circuit is formed by connecting a set of series resistors in parallel.

Connect \(R_1\) and \(R_2\) in series to get an effective resistance of \(R_{S1}\).
Similarly, connect \(R_3\) and \(R_4\) in series to get an effective resistance of \(R_{S2}\).
These series segments of resistors are then joined in parallel.

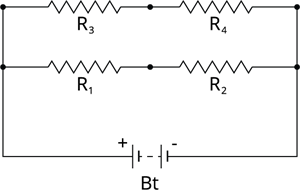
Parallel-series combination of resistors

Using the effective resistance of the series circuit,

R_{S} = R_{1} + R_{2} + R_{3}

, we get,

\begin{array}{l} R_{S1} = R_{1} + R_{2} \\ R_{S2} = R_{3} + R_{4} \end{array}

Using the formula for the effective resistance of the parallel combination of resistors,

\frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}

, the net effective resistance of the parallel-series combination of resistors is,

\frac{1}{R_{Total}} = \frac{1}{R_{S 1}} + \frac{1}{R_{S 2}}

Connections for domestic uses:

We know that the current flowing in a series circuit is always constant. For domestic purposes, it seems practically impossible to use series circuits. For example, electric light and an electric heater cannot be connected in series because they require currents of vastly different values to function effectively.

Also, if the circuit is broken or disturbed at any point, the current cannot flow through the appliances, and hence it will not function. It is one of the major disadvantages of a series circuit.

Importance of parallel connection:

All the electric circuits in a house are connected in parallel. The connections are made in parallel so that the removal of one circuit does not impact the other circuits. Another benefit of connecting circuits in parallel is that each electrical appliance receives the same amount of voltage. Hence, parallel connections are preferred for domestic purposes.

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

18. Combination of series and parallel connections

Theory: