PDF chapter test TRY NOW
To understand the concept of refraction of light through a glass slab, let us do an activity.
- Using drawing pins, fix a sheet of white paper on a drawing board.
- Cover the sheet in the middle with a rectangular glass slab.
- With a pencil, trace the slab's outline.
- Let us name the sketch as \(ABCD\).
- Take four identical pins and arrange them in a row.
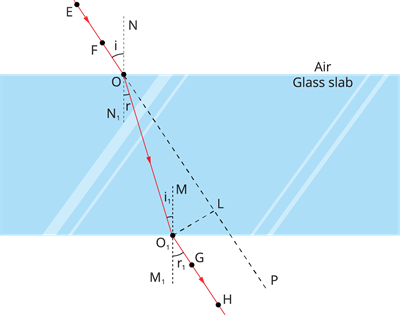
- Fix two pins vertically, say \(E\) and \(F\), so that the line connecting them is inclined to the edge \(AB\).
- Look through the opposite edge for the images of pins \(E\) and \(F\).
- Fix two additional pins, say \(G\) and \(H\), so that they form a straight line along with the images of \(E\) and \(F\). Remove the slab and pins.
- Make a line up to \(AB\) by joining the positions of the tips of the pins \(E\) and \(F\). Let \(EF\) meet \(AB\) at \(O\).
- Similarly, join the positions of the tip of the pins G and H and produce it up to the edge \(CD\).
- Let \(HG\) meet \(CD\) at \(O′\).
- Join \(O\) and \(O′\).
- Also, produce \(EF\) up to \(P\), as shown by a dotted line in the below diagram.
Refraction through a glass slab
You will notice that the light ray has changed direction at points \(O\) and \(O′\) in this activity. Both the points \(O\) and \(O′\) are located on surfaces that separate two transparent media. At \(O′\), draw a perpendicular \(NN'\) to \(AB\) and a perpendicular \(MM′\) to \(CD\). At point \(O\), the light ray has crossed from a rarer medium to a denser medium, i.e., from air to glass.
In this case, the light rays bend towards the normal. The light ray has crossed from glass to air at \(O′\), moving from a denser to a rarer medium. The light ray moves away from the normal in this case. At both refracting surfaces \(AB\) and \(CD\), compare the angle of incidence with the angle of refraction. The incident ray is a ray that is obliquely incident on the surface \(AB\). The refracted ray is \(OO′\), and the emergent ray is \(O′ H\).
You will notice that the emergent ray follows the same path as the incident ray. At the opposite parallel faces \(AB\) (air-glass interface) and \(CD\) (glass-air interface) of the rectangular glass slab, the extent of bending the ray of light is equal and opposite. The ray emerges parallel to the incident ray as a result of this. However, the light ray is slightly shifted to the side.
What happens when a light ray is an incident normally on the interface of two media? Let us try to figure it out in the next section.
