PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn the previous sections, we learned magnetic field lines produced by a current-carrying circular loop.
In this section, we will observe the pattern of the magnetic field produced by a current-carrying circular coil.
Steps:
- Take rectangular cardboard which has two holes.
- Insert a circular coil having a large number of turns through the holes (normal to the cardboard plane).
- Join the ends of the coil in series with a battery, key, and rheostat (variable resistance), as shown in the below figure.
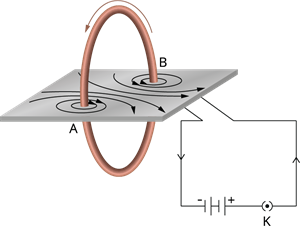
Magnetic field produced by a current-carrying circular coil
- Spray iron filings uniformly on the cardboard. (You may use a salt sprinkler to spray.)
- Plug the key
- Tap the cardboard mildly a few times.
- Observe the pattern of the iron filings that emerges on the cardboard.
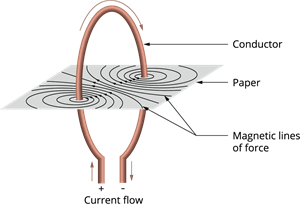
Pattern of the magnetic field produced by a current-carrying circular coil
Observations:
The magnitude of the magnetic field produced by a current-carrying circular wire at its centre is:
- Directly proportional to the current passing through the circular wire.
- Inversely proportional to the radius of the circular wire.
- The strength of the magnetic field can be increased by taking a circular coil consisting of a number of turns of insulated copper wire closely wound together.
- If a circular coil has '\(n\)' turns, the magnetic field produced by this current-carrying circular coil will be '\(n\)' times as large as that produced by a circular loop of a single turn of wire.
Register for free to see more content