PDF chapter test TRY NOW
A planet is an astronomical object or a celestial body that orbits a star. Planets do not emit light on their own, whereas they simply reflect the Sun's light that falls on them.
Criteria for a planet:
- It should orbit around the Sun or its respective stars.
- The celestial object should be spherical in shape.
- It should have a clear area around the orbit.
Planets in the solar system:
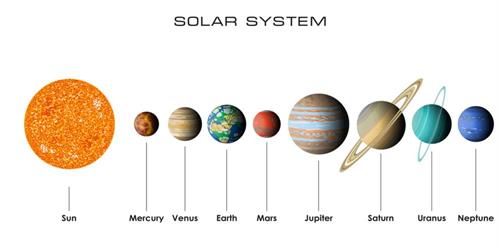
Solar system
These eight planets are categorized as inner planets and outer planets.
Inner planets:
The first four planets that are closer to the Sun are called inner planets. They are Mercury, Venus, Earth, and Mars. These planets are also called terrestrial planets or rocky planets, as they have solid, rocky surfaces.
Inner planets: Mercury, Venus, Earth, and Mars
Outer planets:
The next four planets that are farther away from the Sun are called as outer planets. They are Jupiter, Saturn, Uranus, and Neptune. These four planets are giant balls of gases, and they do not have solid rocky surfaces. Hence, they are called Gas giants or Jovian planets. These planets have a system of rings around them and a large number of satellites.
Outer planets: Jupiter, Saturn, Uranus, and Neptune
Identifying planets:
When we look at the night sky, we don't see the stars alone but also the planets. The main difference between a star and a planet is that the stars twinkle, whereas the planets do not. This is the simplest way to differentiate planets from stars. Planets always change their position with respect to the stars.
Reference:
https://live.staticflickr.com/52/146120442_f5957511fd_b.jpg
Register for free to see more content