PDF chapter test TRY NOW
A family from Pune has been recorded as the tallest family in India. Sharad Kulkarni and his wife Sanjot are the tallest couple in India. The former stands at \(7\)\(ft\) \(1.5\) \(ins\) tall, and the latter stands at \(6ft\) \(2.6\) \(ins\) tall. Even their daughters, Mruga and Sanya, stand above six feet.

This family depicts the laws of genetics that if parents are tall, their offspring has higher possibilities of being tall. What if a tall male marries a short female? This crossing with only one contrasting character is called a Monohybrid cross, which Gregor Mendel experimented with using pea plants.
Monohybrid crosses involve the inheritance of only one pair of contrasting characters.
The monohybrid experiment refers to the crossing of two plants that differ in one character. Mendel chose two pea plants, one with a tall stem and the other with a dwarf or short stem. These plants were considered parental plants (\(P\)) and were used for pure breeding. For example, a cross between tall and dwarf plants is between two forms of a single trait.
Important!
A pure plant is bred true in terms of a specific trait for several generations. The pure breeding tall plant was chosen from a stock that had produced tall plants for many generations. Pure-bred tall and dwarf plants were used as parents and crossed. This crossing is accomplished by first removing a young flower's male parts (anthers) from a tall plant. After that, the flower is wrapped in a small paper bag. The pistil of this flower was dusted with pollen from the dwarf plant as it matured. Seeds collected from these plants were planted, and a group of plants grew from them.
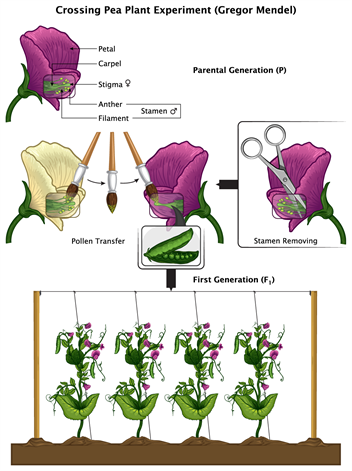
Crossing pea plant experiment
The stages of Mendel's experiments:
- Choosing pure or true-breeding parents (Parental or \(P\)) generation) to produce first-generation plants (First filial or \(F1\) generation)
- \(F1\) plant self-pollination to produce subsequent generations (\(F2\), \(F3\), etc.).
- Hybridisation to produce hybrids refers to the offspring produced by a cross between individuals of the same species who differ in at least one way.
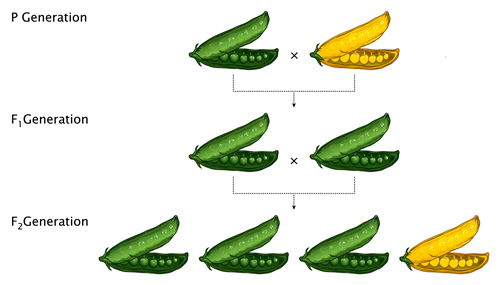
Mendelian inheritance
Mendel's explanation of monohybrid cross
Parental generation: Pure breeding tall plant and a pure breeding dwarf plant.
\(F1\) generation: Plants raised from the seeds of a pure breeding parental cross in the \(F1\) generation were tall and monohybrid.
\(F2\) generation: Selfing of the \(F1\) monohybrids resulted in tall and dwarf plants in a \(3:1\) ratio.
Result: Of the \(1064\) plants, Mendel obtained \(787\) tall plants and \(277\) dwarf plants. That is, \(75\) % of the plants were tall, and \(25\)% were dwarf.
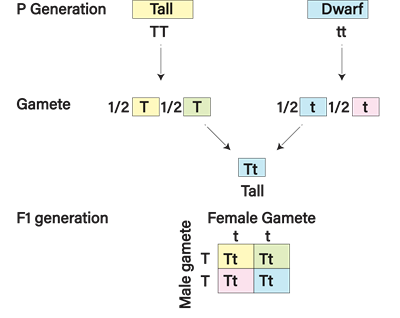
Monohybrid cross
Genotype and phenotype
The tall parent's genotype is \(TT\). The dwarf parent's genotype is \(tt\), while the \(F1\) generation plant's genotype is \(Tt\).
A genotype is the genetic expression of an organism.
(or)
A genotype refers to a plant's or animal's genetic makeup or gene content.
Phenotype refers to a plant's or animal's external visible appearance.
(or)
A genotype refers to a plant's or animal's genetic makeup or gene content.
Phenotype refers to a plant's or animal's external visible appearance.
In the \(F2\) generation \(3\) distinct types were obtained:
- Tall Homozygous – \(TT\) (Pure) – \(1\)
- Tall Heterozygous – Tt – \(2\)
- Dwarf Homozygous – \(tt\) (Pure) – \(1\)
There are three genotypically distinct types of plants in Mendel's \(F2\) generation. They are \(25\)% \(TT\) (homozygous), \(50\) % \(Tt\) (heterozygous), and \(25\ \)% \(tt\), respectively (homozygous). Because it depends on the genetic makeup of individuals, this ratio is known as the genotypic ratio. Hence the genotypic ratio is \(1:2:1\).
Phenotype is known as the external expression of a specific trait. It excludes the unexpressed traits caused by recessive genes. The \(F2\) generation in Mendel's experiment has two types of plants phenotypically. They are both tall and short. The tall and the dwarf are observed in a
\(3:1\) ratio. The ratio is known as the phenotypic ratio.
- Tall homozygous & Tall heterozygous (\(TT\) and \(Tt\)) - \(3\)
- Dwarf Homozygous (\(tt\)) - \(1\)
Hence the phenotypic ratio is \(3:1\).
Important!
Johannsen coined the terms genotype and phenotype.
Mendel stated that each organism consists of a set of characteristics. ''He denoted that a pair of factors or determiners determine each character''. These factors are now known as genes. A gene determines an organism's biological characteristics. It serves as a functional unit of heredity. So a gene is a unit of \(DNA\) that is responsible for a character's appearance and inheritance.
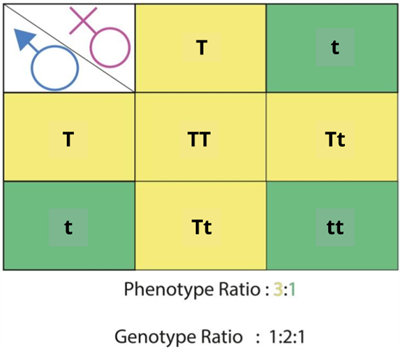
Phenotypic and genotypic ratios of a monohybrid cross
Mendel has seen the pea plant's height as the main character in his experiment. He crossed a tall plant with a dwarf plant. The \(F1\) plants that resulted were tall. Mendel referred to the (tall) character that appeared in the \(F1\) generation as the dominant character. The recessive character was named after the other character (dwarf), masked by the dominant character in the \(F1\) generation.
The character which expresses itself is called the dominant (Tallness) condition, and that which is masked is called a recessive condition (Dwarfness).
The masked recessive character did not disappear; rather, it reappeared in the \(F2\) generation.
The factors that determined dominant characters were known as dominant factors, and those that determined recessive characters were known as recessive factors.
In this experiment, the dominant character, i.e., the plant's tallness, was controlled by the dominant factor, whereas the recessive character, or dwarfness, was controlled by recessive factors.
To visualise how genes or factors are transmitted and distributed, it is helpful to represent the genes with alphabets. The dominant gene is named after the first letter of the dominant character, and the recessive gene is named after the second letter of the dominant character.
Tallness is the dominant trait in the monohybrid cross, and dwarfism is the recessive trait. So, \(T\) represents the dominant gene, and \(t\) represents the recessive gene.
Important!
"A pair of factors or genes already determine each characteristic of an organism."
Hence, \(TT\) represents the pure breeding tall plant, and \(tt\) represents the pure breeding dwarf plant. These plants produce gametes through gametogenesis. Gametes segregate or separate so that each gamete receives a single factor from a pair of factors responsible for the expression of a specific character.
Thus, each gamete will receive only one of a character's two genes. As a result, tall plant gametes contain a single dominant gene, \(T\), while dwarf plant gametes contain a single recessive gene, \(t\).
\(F1\) generation
When pure breeding tall and dwarf plants cross, the female gamete with the dominant gene, \(T\), is fertilised by a male gamete with the recessive gene, \(t\) or vice versa. The resulting \(F1\) generation plants contain \(Tt\). In these plants, the dominant gene, \(T,\) masks the expression of the recessive gene, \(t\). Hence all \(F1\) plants are tall.
\(F1\) plants \(Tt\) produce two types of gametes: Those with the dominant gene \(T\) and those with the recessive gene \(t\). These gametes are produced in equal numbers, i.e., \(50\) % of the gametes contain \(T\), and the other \(50\) % of the gametes contain \(t\).
\(F2\) generation
\(F1\) male and female gametes combine at random, yielding four possible combinations. \(TT\), \(Tt\), \(Tt\), and \(tt\) are the four possible combinations. The plants are tall because the first three combinations (\(TT\), \(Tt\), \(Tt\)) contain dominant genes. Because the fourth combination (\(tt\)) lacks a dominant gene, the plant is dwarf. So, in the \(F2\) generation, three-fourths of the plants are tall, and one-fourth are dwarf, implying that tall and dwarf plants occur in a \(3:1\) ratio.
A video explaining monohybrid genetic cross
Reference:
https://commons.wikimedia.org/wiki/File:Figure_12_02_02.png
https://upload.wikimedia.org/wikipedia/commons/4/47/Heterozygous.jpg
https://upload.wikimedia.org/wikipedia/commons/2/21/Alleles_on_gene.jpg
