Newton’s universal law of gravitation — lesson. Science State Board, Class 10.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Newton’s universal law of gravitation:

This law states that every particle of matter in this universe attracts every other particle with force.

The force between the particles is always attractive, and it does not depend on the medium where they are placed.

Let

m_{1}

and

m_{2}

be the masses of two bodies \(A\) and \(B\), placed \(r metre\) apart in space.

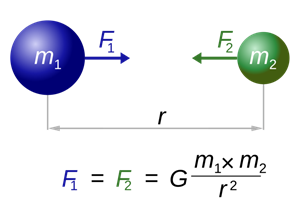
The gravitational force between two masses

This force of attraction is directly proportional to the multiplication of their masses (

m_{1}

and

m_{2}

) and inversely proportionate to the square of the distance between the centres (

r^{2}

) of these masses. This force acts in the direction along the line connecting the masses.

\begin{array}{l} Force (F) \propto m_{1} \times m_{2} \\ F \propto \frac{1}{r^{2}} \end{array}

On combining the above two expressions,

\begin{array}{l} Force (F) \propto \frac{m_{1} \times m_{2}}{r^{2}} \\ Force (F) = \frac{G \times m_{1} \times m_{2}}{r^{2}} \end{array}

Where,

\(G\) is the universal gravitational constant.

The SI unit of universal gravitational constant is

N m^{2} {kg}^{- 2}

, and its value is

6.674 \times 10^{- 11} N m^{2} {kg}^{- 2}

Did you find an error?

19. Newton’s universal law of gravitation