
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn the previous section, we learned Newton's law of gravitation. In this section, we will discuss acceleration due to gravity (\(g\)) and its relation with universal gravitational constant (\(G\))
Acceleration due to gravity (\(g\)):
Whenever you throw any object upwards, its velocity terminates at a particular height, and then it falls down due to the Earth's gravitational force. The velocity of the object continuously changes as it falls down. This change in velocity is undoubtedly due to the force acting on the object. The acceleration of the body is because of the Earth's gravitational force.
So, it is known as 'acceleration due to the gravitational force of the Earth' or 'acceleration due to gravity of the Earth'. It is represented as '\(g\)'. Its unit is .
The average value of the acceleration due to gravity is taken as \(9.8\) on the surface of the Earth. This means that the velocity of a body during the downward free-fall motion varies by \(9.8\) for every \(1\) \(second\). However, the value of '\(g\)' is not the same at all points on the surface of the Earth.
But '\(g\)' can be expressed in CGS also, where the value will be \(981\) \(cm s^{-2}\). So here the unit is \(cm s^{-2}\). So, the unit of '\(g\)' can also be expressed as \(cm s^{-2}\).
Relation between \(g\) and \(G\):
When an object rests on the surface of the Earth, it is acted upon by the Earth's gravitational force.
Let us calculate the magnitude of this force in two ways.
Let '\(M\)' be the mass of the Earth, and '\(m\)' be the mass of the object.
The whole mass of the Earth is considered to be concentrated at its centre.
The radius of the Earth (\(R\)) \(= 6378\ km\) (\(6400\ km\) approximately).
By Newton's law of gravitation, the force that acts on the object is given by,
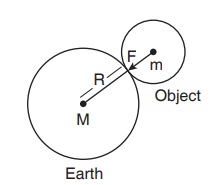
Relation between g and G
Here, the radius of the object is assumed to be negligible compared with the radius of the Earth.
Now, the same force can be calculated by using Newton's second law of motion.
According to this law, the force acting on the object is provided by the product of its mass and acceleration (also known as weight).
Here, the acceleration of the object is under the action of gravity; hence \(a\ =\ g\)
Comparing Eq. (1) and (2), we get,
The relationship between \(g\) and \(G\) is expressed in the above equation.