PDF chapter test TRY NOW
A tall beaker is filled with liquid so that it forms a liquid column. The area of the cross-section at the bottom is \(A\). The density of the liquid is denoted by \(ρ\), and the height of the liquid column is \(h\). In other words, the depth of the water from the top-level surface is \(h\).
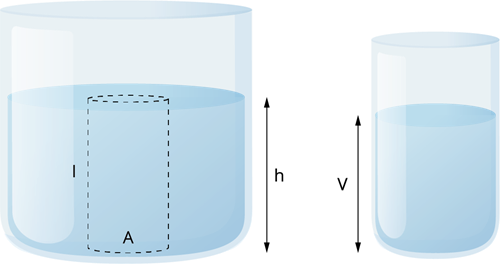
Pressure due to a liquid column
We know that thrust at the bottom of the column is equal to the weight of the liquid. It is mathematically represented as
We can get the mass of liquid by multiplying volume of the liquid by its density.
Volume of the liquid column,
Substitute equation \(3\) in \(2\),
Substitute equation \(4\) in \(1\),
Now, apply it in the pressure formula
Therefore, Pressure due to liquid column \(=\)
The above expression shows that pressure in a liquid column is determined by depth, the density of the liquid and theacceleration due to gravity. However, the final expression for pressure does not have the term area \(A\) in it. Thus, pressure in a liquid depends on depth only.
Example:
1. Calculate the pressure exerted by a column of water of height \(0.9\) \(m\). (Density of water \(=\) \(1000\) \(kg\) \({m}^-3\)).
Given:
The height or depth of the column is \(0.9\).
Density of the water is \(1000\)
To find: Pressure
Pressure \(=\)
Apply the known values,
