PDF chapter test TRY NOW
Let us do an activity to understand Archimede's principle,
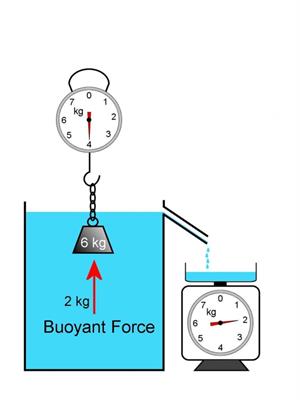
- Tie one end of a string or spring balance to a piece of stone.
- Hang the stone by holding the hook of the balance or the string.
- Note the elongation of the string or the measurement on the spring balance due to the weight of the stone.
- Now, slowly dip the stone in the water in a container.
Archimedes' principle
You can notice that the elongation of the string or the spring balance reading decreases when the stone or weight is gradually lowered in the water. However, there will be no further change when the stone gets fully immersed in the water.
What do you understand from the decrease in the extension of the string or the reading of spring balance?
We know that the elongation or extension produced in the string or the spring balance is due to the weight of the stone. Since the extension decreases once the stone starts to immerse in water, some force acts on the stone in an upward direction. As a result, the net force on the string decreases, the elongation also decreases. As discussed earlier, this upward force exerted by water is known as the force of buoyancy.
We know that the elongation or extension produced in the string or the spring balance is due to the weight of the stone. Since the extension decreases once the stone starts to immerse in water, some force acts on the stone in an upward direction. As a result, the net force on the string decreases, the elongation also decreases. As discussed earlier, this upward force exerted by water is known as the force of buoyancy.
What is the measure of the buoyant force experienced by a body? Is it the same in all fluids for a particular body? Do all bodies in a given fluid experience the same buoyant force?
Archimedes’ principle, stated as follows, contain the answer to these questions:
When a body is immersed fully or partially in a fluid, it experiences an upward force equal to the weight of the fluid displaced by it.
The apparent weight of an object can be found by using the below formula,
Archimedes’ principle has a lot of applications in real life. It is used in designing ships, aeroplanes and submarines. A lactometer and hydrometer, which determine milk sample purity and the density of liquids, respectively, work on the Archimedes principle.
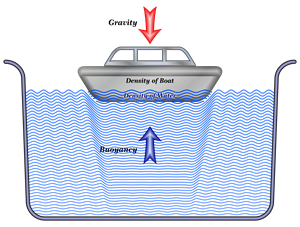
Archimedes' principle in the design of ships

Archimedes' principle
Archimedes, a Greek scientist, discovered the principle after noticing that the water in a bathtub overflowed when he stepped into it. He rushed through the streets shouting “Eureka!”, which means “I have got it”.
This knowledge leads him to find the purity of the gold in the crown made for the king. His work in the field of mechanics and geometry made him famous. His understanding of levers, pulleys, wheels, and-axle helped the Greek army fight against the Roman army.
This knowledge leads him to find the purity of the gold in the crown made for the king. His work in the field of mechanics and geometry made him famous. His understanding of levers, pulleys, wheels, and-axle helped the Greek army fight against the Roman army.
